（第11回）レムニスケート曲線の5等分—ガウスの遺稿より
数学の泉（高瀬正仁）｜ 2019.08.02
数学に泉あり。数学は大小無数の流れで構成されていて、今も絶え間なく流れ続けている雄大な学問ですが、どの流れにも源泉があり、しかもその源泉を作った特定の人物が存在します。共感と共鳴。数学の泉の創造者たちの心情と心を通わせることこそが、数学を理解するという不思議な体験の本質です。そこで数々の泉を歴訪して創造の現場に立ち会って、創造者の苦心を回想し、共感し、共鳴する糸口を目の当たりにすることをめざしたいと思います。(毎月上旬更新予定)
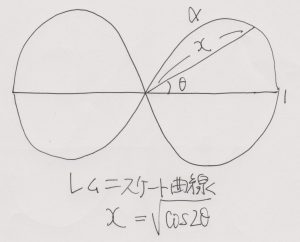
今日の楕円関数論はレムニスケート曲線x=√cos2θ (図1)の発見とともに始まりました．
図1
レムニスケート曲線の弧長はレムニスケート積分という名の楕円積分
α=∫x0dx√1−x4により表されます．この積分の逆関数
x=φ(α)は 1 価関数で，レムニスケート関数と呼ばれています．レムニスケート関数はオイラーには見られませんが，アーベルの論文「楕円関数研究」(1827∼28年)においてはじめて基礎的な諸性質が繰り広げられました．アーベルに先立って，ガウスもまたレムニスケート関数に着目しています．公表にいたらなかったものの，ガウスの遺稿には多くの記述が遺されています．