出題（2019年12月号掲載分）／応募締切（12月8日）／解答（2020年3月号掲載）
出題1
16 個の整数
\begin{align*}
0,\, 0,\, 0,\, 0,\, 0,\, 0,\, 0,\, 0,\, 1,\, 1,\, 1,\, 1,\, 1,\, 1,\, 1,\, 1
\end{align*}の中からどの 9 個を選んでも，その和は 9 の倍数にならない．同様のことは 17 個の整数でも可能だろうか？ つまり 17 個の整数をうまく選んで，その中のどの 9 個の和も 9 の倍数ではないようにできるか？
出題：徳重典英
出題2
平面(ユークリッド平面)内の有限個の点からなる集合 $P$ (以後，配置とよぶ)に対して，$P$ に属する相異なる二点を結んでできる線分同士の交点として得られる点を $P$ に追加した集合を $T(P)$ と定義します(線分の交点とは，二つの線分の共通部分が一点となるときのその一点のことをいうこととします)．$T_0(P)= P$, $T_1(P)=T(P)$, $T_2(P)=T (T(P))$, $T_3 (P) =T(T(T(P)))$, $\cdots$ と $T$ を $n$ 回繰り返して得られる集合を $T_n(P)$ とし，これらすべての和集合を $P_\infty=\bigcup\limits^\infty_{n=0}T_n(P)$ とおきます．$P_\infty$ が有限集合であるときに $P$ は有限配置であるとよび，$P_\infty$ が無限集合であるときに $P$ は無限配置であるとよぶことにします．
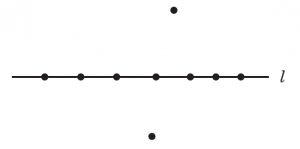
図1のように，直線($l$ とします)上に有限個の点が並び，$l$ によって分けられる二つの半平面のそれぞれに，$l$ 上にない点が高々一点のみ存在するような配置のことを「$\div$ 配置」とよびましょう．「高々一点」ということに注意してください(例えば一つの直線上に有限個点が並んでいる配置も $\div$ 配置です)．
図1
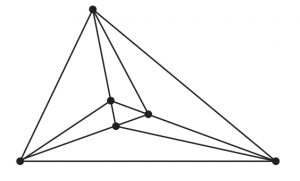
また，図2のように三角形の中に三角形があり，小さな三角形の二頂点と大きな三角形の一つの頂点が同一直線上にあるような六点からなる配置を「手裏剣配置」とよびます．
図2
このとき，配置 $P$ が有限配置であるための必要十分条件は，「$P$ が $\div$ 配置または手裏剣配置」であることを証明してください．
出題：関真一朗
応募規定［解答掲載2020年3月号］
郵送の場合
B5版の用紙をご使用のうえ，解答用紙 l 枚ごとにA：出題の番号(例：12月号出題1)，B：住所，氏名(ふりがなも明記，誌上での仮名を希望される方は，こちらに明記)，年齢，職業を記入して，下記宛先までお送りください．
〒170-8474 東京都豊島区南大塚3-12-4
日本評論社 数学セミナー〈エレガントな解答をもとむ〉係
メール送信の場合
B5版のサイズで，解答用紙 l 枚ごとにA：出題の番号(例：12月号出題1)，B：住所，氏名(ふりがなも明記，誌上での仮名を希望される方は，こちらに明記)，年齢，職業を記入して，下記フォームから PDF ファイルを送信して下さい．
解答記載に LaTeX ご利用の方は，テンプレートもご活用下さい．テンプレート利用は任意です．またテンプレートの漢字コードはUTF8です．ファイルが文字化けするときは適宜変換してお使いください．
投稿フォームが上手く動かないなどの場合は，susemi_elegant@nippyo.co.jp に直接お送り下さい．
注意事項
- 締切：2019年12月8日
- 二題に応募されるときは，郵送の場合は解答用紙を，メール送信の場合はファイルを，出題ごとにかえてください．
- 年齢を忘れずにお書きください．
- 解答用紙は両面の使用を不可とします．
- 解答用紙はご返却できません．
- 問題のご感想も歓迎します．
- 出題掲載号：数学セミナー2019年12月号
- 解答・講評は，本誌2020年3月号にてご確認ください．