出題（2020年2月号掲載分）／応募締切（2月8日）／解答（2020年5月号掲載）
出題1
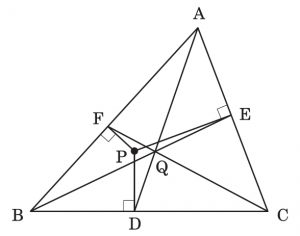
△ABC に対し，同じ平面上の点 P からその 3 辺 BC,CA,AB または延長上に引いた垂線の足(垂線とその辺との交点)を，それぞれ D,E,F とします．もしもこれらがチェバ系のとき，すなわち 3 直線 AD,BE,CF が同一点 Q で交わるとき，点 P を垂足チェバ点とよぶことにします．その軌跡 Γ は一般に 3 次曲線であり，次の諸点を通ります：
3 個の頂点，内心，外心，垂心，3 個の傍心．(重心は二等辺三角形でなければ通りません．)
問1 オイラー線(外心，重心，垂心を通る直線)とこの曲線 Γ との交点は(不等辺三角形なら) 3 点あります．そのうち2点は外心と垂心です．残る第 3 の交点は，△ABC に関してどのような点でしょうか？
問2 △ABC が正三角形なら Γ は 3 本の対称軸に退化します．(これはほぼ自明で，証明する必要はありません．) 正三角形でない二等辺三角形のときには，Γ は対称軸とそれを対称軸の一つとする双曲線とに分解されることを示してください．
注 問1，問2 は別の問題です．どちらか一方だけでも構いません．
出題：一松 信
出題2
要素数が同じ有限集合 A,B に対して(ただし，A∩B=∅)，直積 A×B={(a,b)|a∈A,b∈B} の部分集合 X として任意のものを考えます．このとき，各要素 z∈A∪B に文字列 s(z) を割り当てて，次の条件を満たすようにできることを証明してください．
(a,b)∈X であるとき，そして，そのときに限り，s(a) の後側と s(b) の前側が重なりを持つ．
「s(a) の後側と s(b) の前側が重なりを持つ」という部分をより正確に述べると，以下のようになります．文字列 s(a) の i 番目の文字を s(a)[i] と書くことにします．いま，s(a) の長さが ℓ であり，s(b) の長さが m であるとき，あるi∈{1,2,⋯,min が存在して，任意の j\in\{1,2,\cdots,i\} に対して s(a)[\ell-i+j] = s (b)[j] が成り立つことを「s(a) の後側と s(b) の前側が重なりを持つ」ことと定義します．
余力がある場合は，|A| の要素数が n であるとき，上のような各文字列の長さを 2^n 以下にできることも証明してください．使用する文字種(アルファベット)は有限であれば何でも構いません．
例えば，A=\{a,a’\},\,B=\{b,b’\} で，X=\{(a,b),(a,b’),(a’,b’)\} であるときは，s(a)=\mathsf{st},\,s(a’)=\mathsf{str},\,s(b)=\mathsf{t},\,s(b’)=\mathsf{str} とすればよいです．
出題：岡本吉央
応募規定［解答掲載2020年5月号］
郵送の場合
B5版の用紙をご使用のうえ，解答用紙 l 枚ごとにA：出題の番号(例：2月号出題1)，B：住所，氏名(ふりがなも明記，誌上での仮名を希望される方は，こちらに明記)，年齢，職業を記入して，下記宛先までお送りください．
〒170-8474 東京都豊島区南大塚3-12-4
日本評論社 数学セミナー〈エレガントな解答をもとむ〉係
メール送信の場合
B5版のサイズで，解答用紙l枚ごとにA：出題の番号(例：2月号出題1)，B：住所，氏名(ふりがなも明記，誌上での仮名を希望される方は，こちらに明記)，年齢，職業を記入して，下記フォームから PDF ファイルを送信して下さい．
解答記載に LaTeX ご利用の方は，テンプレートもご活用下さい．テンプレート利用は任意です．またテンプレートの漢字コードはUTF8です．ファイルが文字化けするときは適宜変換してお使いください．
投稿フォームが上手く動かないなどの場合は，susemi_elegant@nippyo.co.jp に直接お送り下さい．
注意事項
- 締切：2020年2月8日
- 二題に応募されるときは，郵送の場合は解答用紙を，メール送信の場合はファイルを，出題ごとにかえてください．
- 年齢を忘れずにお書きください．
- 解答用紙は両面の使用を不可とします．
- 解答用紙はご返却できません．
- 問題のご感想も歓迎します．
- 出題掲載号：数学セミナー2020年2月号
- 解答・講評は，本誌2020年5月号にてご確認ください．