出題（2020年4月号掲載分）／応募締切（4月8日）／解答（2020年7月号掲載）
出題1
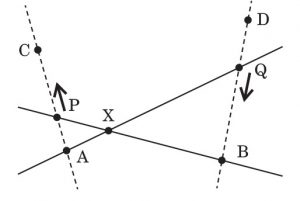
時刻 $t$ に伴って平面上を等速度で動く動点 $\t P$ と $\t Q$ があり，時刻 $t = 0$ のとき，$\t P=\t A,\,\t Q =\t D$ であり，時刻 $t=1$ のとき，$\t P=\t C,\, \t Q =\t B$ であるとします．また，時刻 $t$ はすべての実数に渡って動くものとします．
このとき，直線 $\t{AQ}$ と直線 $\t{BP}$ の交点 $\t X$ となる点の集合を表す式を求めてください．ただし，点 $\t C$，点 $\t D$ は直線 $\t{AB}$ 上にないものとします．
$4$ 定点 $\t A,\,\t B,\t C,\,\t D$ の座標や位置ベクトルを示す文字を好きに設定していただいてかまいません．また式は，座標による式でも，ベクトルによる式でもかまいません．なるべくエレガントな式表現を期待します．
出題：濵中裕明
出題2
平面上にある点の集合 $S$ に対し，次の $3$ つのルールで何本かの線を引くことを考える．
- 各線は $S$ のある点からスタートし，$S$ の点をちょうど $1$ つ通過し $S$ の点で終わる．
- 線同士は $S$ の点以外で交差しない(各線は自分自身とも $S$ の点以外では交差できない)．
- $S$ の各点で線の出入りは合計 $3$ 回まで可能である．
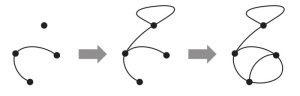
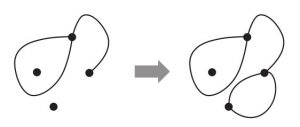
例えば図1 のように進行すると，$3$ 本の線を引いた時点ですべての点で線の出入りがちょうど $3$ 回行われ，これ以上線が引けなくなる．特に，各線はスタートの点を通過したり，$S$ の同じ点に戻ってきたりしてもよいことに注意されたい．一方で図2 のように進行すると，線を $2$ 本引いた時点で線が引けなくなってしまう．
(1) $S$ が $6$ 点のとき，最大で何本の線が引けるか？
(2) $S$ が $6$ 点のとき，それ以上線が引けなくなるまでに少なくとも何本の線を引く必要があるか？
図1 $S$ が $4$ 点のときの進行の例
図2 $S$ が $4$ 点のときの進行の別の例
余裕のある方は，$S$ が $n$ 点のときも考えてみてください．
出題：小関健太＋阿部敏生
応募規定［解答掲載2020年7月号］
郵送の場合
B5版の用紙をご使用のうえ，解答用紙 l 枚ごとにA：出題の番号(例：4月号出題1)，B：住所，氏名(ふりがなも明記，誌上での仮名を希望される方は，こちらに明記)，年齢，職業を記入して，下記宛先までお送りください．
〒170-8474 東京都豊島区南大塚3-12-4
日本評論社 数学セミナー〈エレガントな解答をもとむ〉係
メール送信の場合
B5版のサイズで，解答用紙l枚ごとにA：出題の番号(例：4月号出題1)，B：住所，氏名(ふりがなも明記，誌上での仮名を希望される方は，こちらに明記)，年齢，職業を記入して，下記フォームから PDF ファイルを送信して下さい．
解答記載に LaTeX ご利用の方は，テンプレートもご活用下さい．テンプレート利用は任意です．またテンプレートの漢字コードはUTF8です．ファイルが文字化けするときは適宜変換してお使いください．
投稿フォームが上手く動かないなどの場合は，susemi_elegant@nippyo.co.jp に直接お送り下さい．
注意事項
- 締切：2020年4月8日
- 二題に応募されるときは，郵送の場合は解答用紙を，メール送信の場合はファイルを，出題ごとにかえてください．
- 年齢を忘れずにお書きください．
- 解答用紙は両面の使用を不可とします．
- 解答用紙はご返却できません．
- 問題のご感想も歓迎します．
- 出題掲載号：数学セミナー2020年4月号
- 解答・講評は，本誌2020年6月号にてご確認ください．