（第1回）ちょっと文学的
文学を読んでいても，人文・社会系の本を読んでいても，ついつい数学の目で見てしまい，いつの間にか話が数学になってしまいます．意外や意外，数学の話題が溢れているのです．数学者になってしまったばかりに気になってしまうことを日常生活のひとこまや読書を通じてご紹介していきます．ときどきはディープな話題に迷い込むかもしれません．古典を読んだり，人文系の本を読んだりするときに，数学は案外と身近なものだと改めて気づくことがあります．また数学の知識があると「読書をさらに楽しめる」ことがあるように思います．
たとえば『万葉集』巻第六 (雑歌) にある山部宿禰赤人の反歌 (926) は『原文 万葉集』(上巻)を見ると
安見知之 和期大王波 見吉野乃 飽津之小野笶野上者
跡見居置而 御山者 射目立渡 朝獦尓 十六履起之 夕狩尓
十里蹋立 馬並而御獦曾立為 春之茂野尓
と書かれています．原文を見ると，おや，と思うところがありますね．さりげなく九九が使われています．
また，巻第十一 正述心緒 (2542) には次の歌があります(『原文 万葉集』下巻)．
若草乃 新手枕乎 巻始而 夜哉将間 二八十一不在国
戯書とはいえ，九九が登場していると，ちょっとニンマリしてしまいます．九九では「数学の知識」というには大げさに感じておられるかも知れませんね．
そこで時代は飛んで，樋口一葉の『たけくらべ』を眺めてみます．
あゝ面白くない、おもしろくない、彼の人が來なければ幻燈をはじめるのも嫌、伯母さん此處の家に智惠の板は賣りませぬか、十六武藏でも何でもよい、手が暇で困ると美登利の淋しがれば、夫れよと即坐に鋏を借りて女子づれは切拔きにかゝる
知恵の板が何か知らなければ，読み飛ばしてしまうかもしれません．「知恵の板」は，タングラムというパズルのことです(高木茂男氏による推定 [3])．また「十六武藏」はボードゲームの一種です．そしてタングラム (七巧八分図) は数学パズルや娯楽数学 (数楽) でとてもよく知られているものです．図1を見てください．
図1 (左)タングラム，(中)清少納言知恵の板(右)別の組み方
「タングラム パズル」で検索すると 7 つのピースを並べ替えていろいろな形を作るパターン図が見つかります．少し見方を変えて，「正方形以外の多角形は作れるだろうか」という問いかけをすると，途端に「数学の問題」になります．パズルの中に数学の問題が潜んでいるのです．こういう疑問が沸いたら，まずマーチン・ガードナーの本にあたります．ガードナーの本 [4] によるとタングラムを使って組むことができる (凹んでいない)多角形は 13 種類であることが，F. T. Wang と C.-C. Hsiung により 1942 年に証明が発表されています．
タングラムとは似ているのですが，違うパズルが知られています．「清少納言知恵の板」とよばれるものです．これは清少納言とは何の関係もない単なるあやかり名称のようです ([2] 参照)．図1の中図と右図を見てください．この知恵の板は 2 通りに正方形に組むことができます．タングラムと清少納言知恵の板の性質の違いを調べてみると，いろいろ面白いことがわかります．
まず清少納言知恵の板では釘抜きという形が作れます(タングラムではできない)．
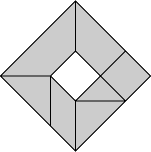
図2 釘抜．パズルショップ・トリトの釘貫の図より転載．
また，タングラムでは「同じ面積である2つの正方形」を組むことができます．清少納言知恵の板では，それができない代わりに「面積比が $1:3$ である正方形と長方形」が組めます．実際に紙でタングラム・清少納言知恵の板を作って試してみてください．
タングラムのときと同様に「どのような多角形が作れるか」を調べるとどうなるでしょうか．数学者の性で，研究論文を探します．Fox-Epstein 先生，上原隆平先生，勝又一穂さんによる研究論文 [5] ではタングラムより多い 16 種作れることが証明されています．
都内に出かけることができたら，東京スカイツリータウン・ソラマチに行って，買い物をしたいと思っています．目的は一心堂本舗の和菓子「東京こはく」(2018年度グッドデザイン賞受賞)．琥珀糖で作られた清少納言知恵板なのです．
参考文献
- 原文 万葉集(上下)，岩波文庫，2016．
- 高木茂男，パズル百科，講談社文庫，1985．
- 高木茂男，清少納言知恵の板とタングラム，数学史研究，162 (1999)，29–41．
- マーティン・ガードナー，ガードナーの数学娯楽(岩沢宏和・上原隆平〔監訳〕)，日本評論社，2015，p.248．
- E. Fox-Epstein, K. Katsumata, R.Uehara, The Convex Configurations of “Sei Shonagon Chie no Ita,” Tangram, and other silhouette puzzles with seven pieces, IEICE Trans. Fundamentals E99-A (2016), no. 6, 1084–1089 (JAIST リポジトリで入手可)．
井ノ口順一（いのぐち・じゅんいち）1967 年千葉県銚子市生まれ．東京都立大学大学院理学研究科博士課程数学専攻単位取得退学．現在，筑波大学数学域教授．
教育学修士(数学教育), 博士(理学)．専門は可積分幾何・差分幾何．
著書に『リッカチのひ・み・つ---解ける微分方程式の理由を探る』(日本評論社, 2010)，『どこにでも居る幾何---アサガオから宇宙まで』(日本評論社, 2010)，『曲線とソリトン』(朝倉書店, 2010)，『常微分方程式NBS』(日本評論社，2015)，『初学者のための偏微分∂を学ぶ』(現代数学社，2019)等．
日本カウンセリング・アカデミー修了, 星空案内人(準案内人), 日本野鳥の会会員．