• #エレガント
• #数セミ
• #数学

 『数学セミナー』のコーナー「エレガントな解答をもとむ」の出題を掲載します．奮ってご応募ください．解答・講評(3ヶ月後)は，本誌にてご確認ください．

(毎月10日頃の掲載予定)

出題1

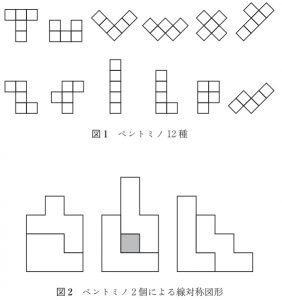
ペントミノは，単位正方形を 5 個つないだ図形で，全部で 12 種あります(図 1)．異なるペントミノを並べて対称図形を作ったりして遊びます．ペントミノの長方形詰めをしているときに，たくさんの対称図形を作ると，一挙にたくさんの解が得られて楽しいですね．

図 2 はペントミノ 2 個による対称図形の例ですが，いずれも線対称です．では，異なるペントミノ 2 個で点対称図形を作ることができるでしょうか．できるならその例を挙げ，不可能ならそのことを証明してください．

点対称，つまり 180 度回転対称とは，図形を 180 度回転したものがもとの図形と一致するということです．また，ペントミノ 2 個は，かならず正方形の辺どうしがぴったり合うように並べることとします．

出題：小谷善行

出題2

$X^n-1$ を整数係数の範囲で完全に因数分解したときに現れる多項式の係数に $0,\, \pm 1$ 以外が現れる最小の $n$ は $105$ であり，その係数が $-2$ であることは，本誌2020 年 10 月号の「せいすうたん」に紹介されています．では係数に，絶対値で $3$ 以上の値の現れる最小の $n$ はいくらになるでしょうか，それを求めてください．

因数分解が完全にできたかの判定には次の事実が役立ちます．

$X^n-1$ は $n$ の各約数に対応した第 $n$ 円分多項式 $\varPhi_n(X)$ の積に分解され，$\varPhi_n(X)$ の次数は $\varphi(n)$ ($n$ 以下の自然数で $n$ と互いに素なものの個数) です．そして各円分多項式はすべて既約な (これ以上分解できない) 多項式です．

次の例は $n = 12$ の場合に，約数 $1,\, 2,\, 3,\, 4,\, 6,\, 12$ の順に表したものです．
$$\begin{align*} X^{12}-1 =(X-1)(X+1)(X^2+X+1)(X^2+1)(X^2-X+1)(X^4-X^2+1) \end{align*}$$

今の時代なら，コンピュータに因数分解をさせようと考えるのも自然でしょう．そのときは，どう進めたらよいかを考えてみてください．たとえば $p$ が奇素数であるとき，$\varPhi_p(X)$ と $\varPhi_{2p}(X)$ の関係を調べておくとよいでしょう．

出題：鈴木治郎

応募規定［解答掲載2021年3月号］

郵送の場合

B5判の用紙をご使用のうえ，解答用紙 l 枚ごとにA：出題の番号(例：12月号出題1)，B：住所，氏名(ふりがなも明記，誌上での仮名を希望される方は，こちらに明記)，年齢，職業を記入して，下記宛先までお送りください．

〒170-8474　東京都豊島区南大塚3-12-4
日本評論社　数学セミナー〈エレガントな解答をもとむ〉係

メール送信の場合

B5判のサイズで，解答用紙l枚ごとにA：出題の番号(例：12月号出題1)，B：住所，氏名(ふりがなも明記，誌上での仮名を希望される方は，こちらに明記)，年齢，職業を記入して，下記フォームから PDF ファイルを送信して下さい(ファイルサイズ10MBまで)．

解答記載に LaTeX ご利用の方は，テンプレートもご活用下さい．テンプレート利用は任意です．またテンプレートの漢字コードはUTF8です．ファイルが文字化けするときは適宜変換してお使いください．

投稿フォームが上手く動かないなどの場合は，susemi_elegant@nippyo.co.jp に直接お送り下さい．

注意事項

• 締切：2020年12月8日
• 二題に応募されるときは，郵送の場合は解答用紙を，メール送信の場合はファイルを，出題ごとにかえてください．
• 年齢を忘れずにお書きください．
• 解答用紙は両面の使用を不可とします．
• 解答用紙はご返却できません．
• 問題のご感想も歓迎します．
• 出題掲載号：数学セミナー2020年12月号
• 解答・講評は，本誌2021年3月号にてご確認ください．

「エレガントな解答をもとむ」をすべて見る
最新の「エレガントな解答をもとむ」はこちら

• #エレガント
• #数セミ
• #数学