出題(2021年2月号掲載分)/応募締切(2月8日)/解答(2021年5月号掲載)
出題1
52=25 は,53=125 の下 2 桁に一致します.また,125 は,55=3125 の下 3 桁に一致します.実は 5n は必ずそれより大きい 5M のある下 k 桁と一致します.
そこで,自然数 n が性質「任意の自然数 m に対して,nm の 10 進表記での桁数を k とするとき,ある自然数 M>m について, nM の下 k 桁が nm と一致する」を満たすか満たさないかを,n=1,2,3,⋯ それぞれについて決定し,理由も添えて答えてください.たとえば 5 はこの性質を満たしますが 10 はこの性質を満たしません.決定できなかった最小の n が大きいほど,より良い解答と見なします.
出題:丹下基生
出題2
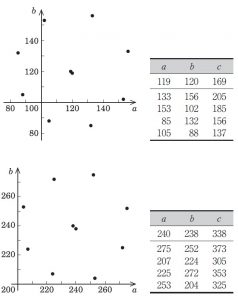
3 辺の長さ a,b,c (c2=a2+b2) がすべて整数である直角三角形をピタゴラス三角形とよびます.この組を多数作り,(a,b) と (b,a) を平面上の直交座標としてプロットすると,しばしば 8 点がほぼ同一円周上に並んで現れます.具体例は下の図 2 枚 (数値はその隣の表;(a,b) を交換した点も含む) です.
問1 しかし下の表の点族は正確に同一円周上には載っていません.そのことを確かめ,何らかの意味でそれらに “最もよく適合する” 円周の方程式を求めてください.
問2 ピタゴラス三角形の組をうまく作ると,上の例のような 8 点の組が,いくらでも正確に同一円周上の点列に近づくようにできることを示してください.
問 1 と問 2 は一応別の課題なので,一方だけの解答でも構いません.ピタゴラス三角形の一般的表現がヒントになります.
出題:一松 信
応募規定[解答掲載2021年5月号]
郵送の場合
B5判の用紙をご使用のうえ,解答用紙 l 枚ごとにA:出題の番号(例:2月号出題1),B:住所,氏名(ふりがなも明記,誌上での仮名を希望される方は,こちらに明記),年齢,職業を記入して,下記宛先までお送りください.
〒170-8474 東京都豊島区南大塚3-12-4
日本評論社 数学セミナー〈エレガントな解答をもとむ〉係
メール送信の場合
B5判のサイズで,解答用紙l枚ごとにA:出題の番号(例:2月号出題1),B:住所,氏名(ふりがなも明記,誌上での仮名を希望される方は,こちらに明記),年齢,職業を記入して,下記フォームから PDF ファイルを送信して下さい (ファイルサイズ10MBまで).
解答記載に LaTeX ご利用の方は,テンプレートもご活用下さい.テンプレート利用は任意です.またテンプレートの漢字コードはUTF8です.ファイルが文字化けするときは適宜変換してお使いください.
投稿フォームが上手く動かないなどの場合は,susemi_elegant@nippyo.co.jp に直接お送り下さい.
注意事項
- 締切:2021年2月8日
- 二題に応募されるときは,郵送の場合は解答用紙を,メール送信の場合はファイルを,出題ごとにかえてください.
- 年齢を忘れずにお書きください.
- 解答用紙は両面の使用を不可とします.
- 解答用紙はご返却できません.
- 問題のご感想も歓迎します.
- 出題掲載号:数学セミナー2021年2月号
- 解答・講評は,本誌2021年5月号にてご確認ください.