出題(2021年9月号掲載分)/応募締切(9月8日)/解答(2021年12月号掲載)
出題1
(1)凸四角形の 4 頂点を通る楕円は多く存在しますが,一般にその中心 (二本の軸の交点) は図のように楕円の選び方に応じて変化します.しかし,最初の凸四角形が特別な場合には,4 頂点を通る楕円の中心は固定されたままになります.そのような凸四角形をすべて求めてください.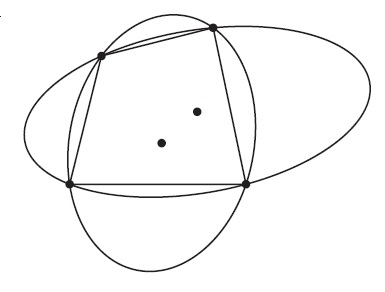
(2) (1)において,「中心」を「二本の軸の傾き」に置き換えて,同じ問題を解いてください.
一問だけの解答も歓迎します.
出題:阿賀岡芳夫
出題2
A={a1,a2,⋯,an} を整数全体 Z の部分集合とします.B={b1,b2,⋯,bn} が A の平行移動であるとは,b1−a1=b2−a2=⋯=bn−an が成り立つことです.
では,与えられた 3 個の整数からなる集合 A={a1,a2,a3} について,A の平行移動のみで Z を分割できる (共通部分のない和集合として書ける) ための必要十分条件を求めてください.例えば,{1,2,4} の平行移動のみで Z を分割することは明らかに不可能です.一方,{1,2,6} を考えると,
Z=⋯∪{−2,−1,3}∪{1,2,6}∪{4,5,9}∪{7,8,12}∪⋯であり,Z は {1,2,6} により分割可能です.
出題:中上川友樹
応募規定[解答掲載2021年12月号]
郵送の場合
B5判の用紙をご使用のうえ,解答用紙 l 枚ごとにA:出題の番号(例:9月号出題1),B:住所,氏名(ふりがなも明記,誌上での仮名を希望される方は,こちらに明記),年齢,職業を記入して,下記宛先までお送りください.
〒170-8474 東京都豊島区南大塚3-12-4
日本評論社 数学セミナー〈エレガントな解答をもとむ〉係
メール送信の場合
B5判のサイズで,解答用紙l枚ごとにA:出題の番号(例:9月号出題1),B:住所,氏名(ふりがなも明記,誌上での仮名を希望される方は,こちらに明記),年齢,職業を記入して,下記フォームから PDF ファイルを送信して下さい (ファイルサイズ10MBまで).
解答記載に LaTeX ご利用の方は,テンプレートもご活用下さい.テンプレート利用は任意です.またテンプレートの漢字コードはUTF8です.ファイルが文字化けするときは適宜変換してお使いください.
投稿フォームが上手く動かないなどの場合は,susemi_elegant@nippyo.co.jp に直接お送り下さい.
注意事項
- 締切:2021年9月8日
- 二題に応募されるときは,郵送の場合は解答用紙を,メール送信の場合はファイルを,出題ごとにかえてください.
- 年齢を忘れずにお書きください.
- 解答用紙は両面の使用を不可とします.
- 解答用紙はご返却できません.
- 問題のご感想も歓迎します.
- 出題掲載号:数学セミナー2021年9月号
- 解答・講評は,本誌2021年12月号にてご確認ください.





