Web日本評論 > 日評雑誌記事セレクション > 出題（2021年10月号掲載分）／応募締切（10月8日）／解答（2022年1月号掲載）

出題（2021年10月号掲載分）／応募締切（10月8日）／解答（2022年1月号掲載）

エレガントな解答をもとむ(数学セミナー)｜ 2021.09.10

『数学セミナー』のコーナー「エレガントな解答をもとむ」の出題を掲載します．奮ってご応募ください．解答・講評(3ヶ月後)は，本誌にてご確認ください．

(毎月10日頃の掲載予定)

$\def\t#1{\text{#1}}\def\dfrac#1#2{\displaystyle\frac{#1}{#2}}\def\bs#1{\boldsymbol{#1}}$

出題1

$n$ を正の整数とし，1 から 6 までの目が等確率で出るサイコロを $n$ 回投げることにします．そのとき，出る目の和が $a$ の倍数となる確率を，$a = 1,\, 2,\, 3,\, 6$ のそれぞれについて計算すると，$n$ がいくつであっても，その値は $\dfrac 1a$ です．それでは，$a = 4,\, 5,\, 7$ の場合はどうでしょうか．それらの場合に，出た目の和が $a$ の倍数となる確率がちょうど $\dfrac 1a$ となるような $n$ はあるでしょうか．$a = 4,\, 5,\, 7$ のそれぞれについて，そのような $n$ がないならないことを証明し，あるならそのような $n$ の一般式を求めてください．

出題者コメント：$7,\, 5,\, 4$ の順に考えたほうがよいかもしれません．3 つのうちの一部だけが解けた場合でも，ぜひ答案を提出してください．推移行列などを使って力ずくで答えを求めることができる方は，得られた答えをより簡潔に導く方法をぜひ考えてみてください．

出題：岩沢宏和

出題2

$n$ を 3 以上の自然数とします．数直線上の $n$ 点集合
\begin{align*}
X=\{a_1,a_2,\cdots,a_n\}\quad (a_1<a_2<\cdots<a_n)
\end{align*}に対し，$X$ の異なる 2 数の差全体の集合を
\begin{align*}
D(X)=\{a_j-a_i\,|\,1\leqq i<j<\leqq n\}
\end{align*}で表し，$D(X)$ の元の個数を $d(X)$ とします．また，$X$ の隣り合った 2 数の差の列
\begin{align*}
(a_2-a_1,a_3-a_2,\cdots,a_n-a_{n-1})
\end{align*}を $X$ の階差列といい $I(X)$ で表します．

ここで $n$ 点集合 $X$ に次の条件 (1), (2) を課すことにします．

(1) $I(X)$ は 1 と無理数 $c$ のみからなる列である．

(2) $I (X) \neq (1,1, \cdots,1)$ かつ $I(X) \neq (c,c, \cdots,c)$.

このような条件をみたす $n$ 点集合 $X$ のうち，$d(X)$ が最小となるものの階差列 $I(X)$ とその最小値 $f(n)$ を答えてください．

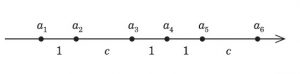
例　下図の $X=\{a_1,a_2,\cdots,a_6\}$ に対し，
\begin{align*}
&I(X)=(1,c,1,1,c),\\[5pt]
&D(X)=\{1, 2, c, 1+c, 2+c, 3+c, 2+2c, 3+2c\}
\end{align*}より $d (X) = 8$ となる．よって，$f(6) \leqq 8$.