出題(2021年11月号掲載分)/応募締切(11月8日)/解答(2022年2月号掲載)
出題1
4 つの頂点位置だけで決まり,最も単純な多面体といえる四面体ですが,その見かけによらずなかなか奥が深い図形です.以下では四面体 T=ABCD の形をさまざまに変化させた際の “最適化問題” を考えます.
(1) T が半径 1 の球に外接するとき,T の外接球の半径 R の最小値を求めてください.
(2) 対辺の積 AB⋅CD,AC⋅BD,AD⋅BC を 3 辺の長さとする三角形 S が存在することを示してください.また,T の体積が 1/3 であるとき,S の面積の最小値を求めてください.
(1) で「T が半径 1 の球に外接する」というのは,T の内接球の半径が 1 であるという意味です.球・四面体・球をマトリョーシカのように入れ子にしたものを,なるべく “薄く” 作りたいという問題になります.両問題ともさまざまな方針が考えられますので,関連した解法に限ることなく,独立に取り組んでもらえればと思います.
出題:鍛冶静雄
出題2
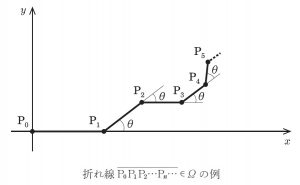
r,θ を 0<r<1,0<θ<π を満たす定数とします.xy 平面に 2 点 P0=(0,0),P1=(1,0) をとり,xy 平面内の折れ線 ¯P0P1P2¯⋯Pn⋯ で次の条件を満たすものを考えます.
- n=1,2,3,⋯ に対して,PnPn+1=rn であり,2 つのベクトル →Pn−1Pn と →PnPn+1 のなす角が θ または −θ である.
このような折れ線の集合 Ω:={¯P0P1P2¯⋯Pn⋯} は,角度に 2 通りの選び方があるので,無限集合です.
Ω の要素であるどの 2 つの折れ線も交差しないとき,r と θ の間に成り立つ関係式を求めてください.
ただし,「折れ線 L1 と L2 が交差する」とは,L1 を構成する一つの線分 ¯PnPn+1 と L2 を構成する一つの線分 ¯P′mP′m+1 であって,次の条件を満たすものが存在することとします.
(1) 2 つの線分は 1 点のみを共有する.
(2) その共有点は,一方の線分の端点ではないか,あるいは Pn+1=P′m+1 である.
出題:時弘哲治
応募規定[解答掲載2022年2月号]
郵送の場合
B5判の用紙をご使用のうえ,解答用紙 l 枚ごとにA:出題の番号(例:11月号出題1),B:住所,氏名(ふりがなも明記,誌上での仮名を希望される方は,こちらに明記),年齢,職業を記入して,下記宛先までお送りください.
〒170-8474 東京都豊島区南大塚3-12-4
日本評論社 数学セミナー〈エレガントな解答をもとむ〉係
メール送信の場合
B5判のサイズで,解答用紙l枚ごとにA:出題の番号(例:11月号出題1),B:住所,氏名(ふりがなも明記,誌上での仮名を希望される方は,こちらに明記),年齢,職業を記入して,下記フォームから PDF ファイルを送信して下さい (ファイルサイズ10MBまで).
解答記載に LaTeX ご利用の方は,テンプレートもご活用下さい.テンプレート利用は任意です.またテンプレートの漢字コードはUTF8です.ファイルが文字化けするときは適宜変換してお使いください.
投稿フォームが上手く動かないなどの場合は,susemi_elegant@nippyo.co.jp に直接お送り下さい.
注意事項
- 締切:2021年11月8日
- 二題に応募されるときは,郵送の場合は解答用紙を,メール送信の場合はファイルを,出題ごとにかえてください.
- 年齢を忘れずにお書きください.
- 解答用紙は両面の使用を不可とします.
- 解答用紙はご返却できません.
- 問題のご感想も歓迎します.
- 出題掲載号:数学セミナー2021年11月号
- 解答・講評は,本誌2022年2月号にてご確認ください.