出題(2022年1月号掲載分)/応募締切(1月8日)/解答(2022年4月号掲載)
出題1
N={1,2,3,⋯} とします.φ:N⟶N が全単射で,任意の n∈N に対して φ(n)=2n または φ−1(n)=2n を満たすとき,φ(4) はいくらですか.また,φ(3) についてはどうですか.
出題:植野義明
出題2
頂点 0 から n−1 を有する図のようなリング状のグラフにおける兎と亀の鬼ごっこを考える.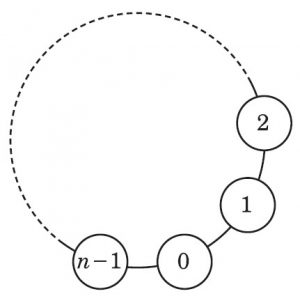
(i)亀の初期位置は頂点 0 とし,時刻 t で頂点 i にいるなら,時刻 t+1 では頂点 i−1,i,i+1 (modn) のどれかに移動できる.
(ii)兎の移動には (初期位置を含めて) 一切制限がない (ジャンプできる).つまり,時刻 t の場所によらず,t+1 では 0 から n−1 の好きな場所にいける.
(iii)兎と亀が異なる頂点にいるときには,相手がどこにいるか見えない.
(iv)ある時刻に両者が同じ頂点にいると兎の負け (捕まってしまう).
(v)兎は亀の戦略 (アルゴリズム) を知っている.したがって,亀のアルゴリズムが決定性であるなら,兎時刻 t における亀の居場所を完全に把握できるので絶対に捕まらない.よって亀は乱数を使う必要がある.
たとえ乱数を使っても,兎は亀のアルゴリズムを解析して,亀が各頂点にいる確率はわかる (ただし互いに相手が見えない約束なので,実際にどの頂点にいるかはわからない).したがって例えば,亀が最初にランダムに左回りか右回りを決め,同じ頂点に留まることなく回りつづけるような簡単なアルゴリズムでは,亀の位置は,時刻 1 では 1 か n−1,時刻 2 では 2 か n−1,のように各時刻 2 箇所の可能性しかあり得ないので,兎は絶対に捕まらない.亀の以下のアルゴリズムに対して,兎のできるだけ良い (捕まる確率の小さい) アルゴリズムを設計し,兎が 2n ステップ以内に捕まってしまう確率を計算せよ.
(1)最初にランダムに頂点を選び,短い方の回り方で移動しそこに留まる.
(2)同様にランダム頂点に移動したあと,時刻 n までそこに留まってから左回りする.
(3) 同様にランダム頂点に時刻 n まで留まって,そのあと再び乱数をつかってランダムに右回りか左回りかを決めその方向に回りつづける.
部分的な解答も歓迎します.
出題:岩間一雄
応募規定[解答掲載2022年4月号]
郵送の場合
B5判の用紙をご使用のうえ,解答用紙 l 枚ごとにA:出題の番号(例:1月号出題1),B:住所,氏名(ふりがなも明記,誌上での仮名を希望される方は,こちらに明記),年齢,職業を記入して,下記宛先までお送りください.
〒170-8474 東京都豊島区南大塚3-12-4
日本評論社 数学セミナー〈エレガントな解答をもとむ〉係
メール送信の場合
B5判のサイズで,解答用紙l枚ごとにA:出題の番号(例:1月号出題1),B:住所,氏名(ふりがなも明記,誌上での仮名を希望される方は,こちらに明記),年齢,職業を記入して,下記フォームから PDF ファイルを送信して下さい (ファイルサイズ10MBまで).
解答記載に LaTeX ご利用の方は,テンプレートもご活用下さい.テンプレート利用は任意です.またテンプレートの漢字コードはUTF8です.ファイルが文字化けするときは適宜変換してお使いください.
投稿フォームが上手く動かないなどの場合は,susemi_elegant@nippyo.co.jp に直接お送り下さい.
注意事項
- 締切:2022年1月8日
- 二題に応募されるときは,郵送の場合は解答用紙を,メール送信の場合はファイルを,出題ごとにかえてください.
- 年齢を忘れずにお書きください.
- 解答用紙は両面の使用を不可とします.
- 解答用紙はご返却できません.
- 問題のご感想も歓迎します.
- 出題掲載号:数学セミナー2022年1月号
- 解答・講評は,本誌2022年4月号にてご確認ください.





