出題（2022年7月号掲載分）／応募締切（7月8日）／解答（2022年10月号掲載）
出題1
今回の問題は，エレ解には珍しい計算問題です．
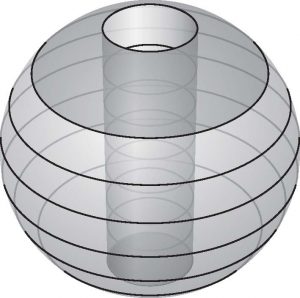
球形のリンゴから，その中心を通る軸をもつ円筒で垂直に芯をくり抜いた残りを，水平な平面で輪切りにして $7$ 人で分けました．きちんと体積が等分されているわけではないですが，僕はリンゴの皮が好きなので一番端をもらいました．直径は小さいけど少し厚みがあって，真横から見た高さが $2\t{cm}$ あり，皮の面積も，芯をくり抜いた残りの $\dfrac{1}{6}$ あります．さて，僕がもらった部分の体積は何 $\t{cm}^3$ でしょうか．また，それは $7$ 人の平均よりも大きいでしょうか．
円周率は $3.14$ で計算してください．できれば，方程式を立てない解答を求めます．なお，ずる賢い解答は嫌いです．
出題：山田修司
出題2
$n$ を 2 以上の整数とします．$n$ 次対称行列 ($n$ 行 $n$ 列の正方行列 $P=(p_{ij})$ で $p_{ij}=p_{ji}$ となるもの) で各成分が非負であり，各行の和が 1 であるもの (各列の和が 1 でもある) を $n$ 次非負対称確率行列と呼ぶことにします．たとえば
\begin{align*}
P=
\begin{pmatrix}
0.2 & 0.3 & 0.5\\
0.3 & 0.2 & 0.5\\
0.5 & 0.5 & 0
\end{pmatrix}
\end{align*}は3次非負対称確率行列です．
対称行列の固有値はすべて実数であることが知られているので，$n$ 次非負対称確率行列$P$の固有値を大きい順に
\begin{align*}
\lambda_1(P)\geqq \lambda_2(P)\geqq \cdots \geqq \lambda_n(P)
\end{align*}と表すことにします．たとえば前の例の $P$ については，$\lambda_1(P)=1$, $\lambda_2(P)=-0.1$, $\lambda_3(P)=-0.5$ となります．
$\lambda_1(P)$ は常に 1 であることが比較的容易にわかりますが，$\lambda_2(P)$ は $P$ ごとに変わります．$\varPi_n$ を $n$ 次非負対称確率行列の集合とするとき，$\varPi_n$ 上の関数 $\lambda_2$ の最小値を求めてください．難しければ，$n$ が 2, 3 くらいの小さい場合だけの応募でも構いません．
出題：栗原大武
応募規定［解答掲載2022年10月号］
郵送の場合
B5判の用紙をご使用のうえ，解答用紙 1 枚ごとにA：出題の番号(例：7月号出題1)，B：住所，氏名(ふりがなも明記，誌上での仮名を希望される方は，こちらに明記)，年齢，職業を記入して，下記宛先までお送りください．
〒170-8474 東京都豊島区南大塚3-12-4
日本評論社 数学セミナー〈エレガントな解答をもとむ〉係
メール送信の場合
B5判のサイズで，解答用紙l枚ごとにA：出題の番号(例：7月号出題1)，B：住所，氏名(ふりがなも明記，誌上での仮名を希望される方は，こちらに明記)，年齢，職業を記入して，下記フォームから PDF ファイルを送信して下さい (ファイルサイズ10MBまで)．
解答記載に LaTeX ご利用の方は，テンプレートもご活用下さい．テンプレート利用は任意です．またテンプレートの漢字コードはUTF8です．ファイルが文字化けするときは適宜変換してお使いください．
投稿フォームが上手く動かないなどの場合は，susemi_elegant@nippyo.co.jp に直接お送り下さい．
注意事項
- 締切：2022年7月8日
- 二題に応募されるときは，郵送の場合は解答用紙を，メール送信の場合はファイルを，出題ごとにかえてください．
- 年齢を忘れずにお書きください．
- 解答用紙は両面の使用を不可とします．
- 解答用紙はご返却できません．
- 問題のご感想も歓迎します．
- 出題掲載号：数学セミナー2022年7月号
- 解答・講評は，本誌2022年10月号にてご確認ください．