出題（2022年9月号掲載分）／応募締切（9月8日）／解答（2022年12月号掲載）
出題1
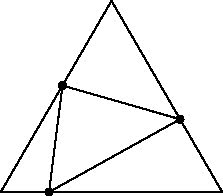
(1) 正三角形の各辺上 (ただし頂点を除く) に 1 点をとってそれらを結ぶと正三角形に内接した三角形ができます．どのような三角形も，このようにして作れることを示してください．
(2) 同様にして，正方形の各辺上 (ただし頂点を除く) に 1 点をとってそれらを結ぶと正方形に内接した凸四角形ができます．しかし正三角形の場合と違って，この方法ですべての凸四角形を作ることはできません．平行四辺形の場合でも，この方法では作ることのできないものがあります．平行四辺形が正方形に内接できるための必要十分条件を，平行四辺形の辺の長さと内角を用いて表してください．
また，内角が順に $\alpha$, $\alpha$, $180^{\circ}-\alpha$, $180^{\circ}-\alpha$ (ただし$45^{\circ} < \alpha < 135^{\circ}$) となる等脚台形は，4 つの内角の大きさを固定した状態のまま辺の長さを変えても，常に正方形に内接できます．(等脚台形の平行な2辺と外枠の正方形の辺の成す角を $45^{\circ}$ にすれば可能です．ただし，正方形の大きさは辺の長さに応じて変化します．) このように，4 つの内角の大きさが固定されたままで辺の長さをいろいろ変えたとき，いつでも正方形に内接できるという性質をもった凸四角形は，等脚台形以外にもあるでしょうか．(長方形や正方形は等脚台形の一種とみなします．)
一問のみの解答，途中までの解答も歓迎します．
出題：阿賀岡芳夫
出題2
(左)$3$-交差，(右) $3$-交差のない配置 ($m=4$, $n=4$)
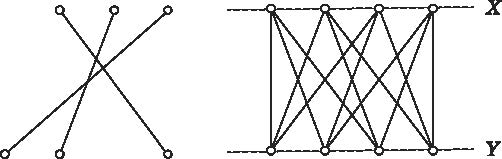
平面上の $k$ 本の線分の集合で，そのうちのどの $2$ 本の線分も互いに交差するような集合を $k$-交差，と呼びます．ここで，$2$ 本の線分はそれらの両端点以外のある $1$ 点を共有する場合に，交差する，とみなすこととします．
平行な $2$ 直線の片方の直線上に $m$ 点の点集合 $X$ があり，もう一方の直線上に $n$ 点の点集合 $Y$ があります．$3$-交差ができないという条件の下で，$X$ と $Y$ を結ぶ線分をなるべく多く引くことを考えます．最大で何本の線分を引くことができるでしょうか？
ゆとりがあれば「$3$-交差ができない」という条件を，「与えられた$2$以上の自然数$k$について$k$-交差ができない」という条件に置き換えた問題も考えてみてください．
出題：中上川友樹
応募規定［解答掲載2022年12月号］
郵送の場合
B5判の用紙をご使用のうえ，解答用紙 l 枚ごとにA：出題の番号(例：9月号出題1)，B：住所，氏名(ふりがなも明記，誌上での仮名を希望される方は，こちらに明記)，年齢，職業を記入して，下記宛先までお送りください．
〒170-8474 東京都豊島区南大塚3-12-4
日本評論社 数学セミナー〈エレガントな解答をもとむ〉係
メール送信の場合
B5判のサイズで，解答用紙 1 枚ごとにA：出題の番号(例：9月号出題1)，B：住所，氏名(ふりがなも明記，誌上での仮名を希望される方は，こちらに明記)，年齢，職業を記入して，下記フォームから PDF ファイルを送信して下さい (ファイルサイズ10MBまで)．
解答記載に LaTeX ご利用の方は，テンプレートもご活用下さい．テンプレート利用は任意です．またテンプレートの漢字コードはUTF8です．ファイルが文字化けするときは適宜変換してお使いください．
投稿フォームが上手く動かないなどの場合は，susemi_elegant@nippyo.co.jp に直接お送り下さい．
注意事項
- 締切：2022年9月8日
- 二題に応募されるときは，郵送の場合は解答用紙を，メール送信の場合はファイルを，出題ごとにかえてください．
- 年齢を忘れずにお書きください．
- 解答用紙は両面の使用を不可とします．
- 解答用紙はご返却できません．
- 問題のご感想も歓迎します．
- 出題掲載号：★★URL★★数学セミナー2022年9月号
- 解答・講評は，本誌2022年12月号にてご確認ください．