Web日本評論 > 日評雑誌記事セレクション > 出題（2023年2月号掲載分）／応募締切（2月8日）／解答（2023年5月号掲載）

出題（2023年2月号掲載分）／応募締切（2月8日）／解答（2023年5月号掲載）

エレガントな解答をもとむ(数学セミナー)｜ 2023.01.10

『数学セミナー』のコーナー「エレガントな解答をもとむ」の出題を掲載します．奮ってご応募ください．解答・講評(3ヶ月後)は，本誌にてご確認ください．

(毎月10日頃の掲載予定)

$\def\t#1{\text{#1}}\def\dfrac#1#2{\displaystyle\frac{#1}{#2}}$

出題1

辺の長さが $3,\, 4,\, 5$ のピタゴラス三角形をつないで凸多角形を作る．それを凸 $N$ 角形としたとき， $N$ の最大値を求めよ．ただし，ピタゴラス三角形はすべて同じ大きさとする．裏返しは可能である．また，多角形の内部にすき間があってはいけない．下に凸七角形の例を示す．

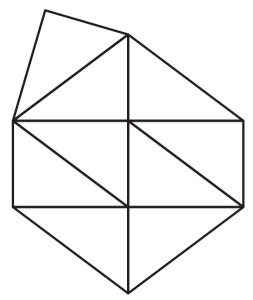
出題：小谷善行

出題2

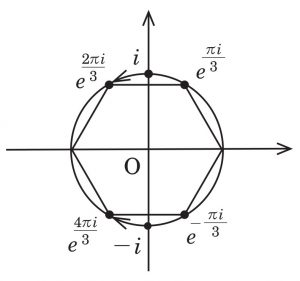
すべての原始 $n$ 乗根を根にもつ既約多項式 $\varPhi_n(t)$ を円分多項式といいます．例えば， $\varPhi_3(t)=t^2+t+1$ や $\varPhi_6(t)=t^2-t+1$ となります．この場合， $2$ つの根はそれぞれ，絶対値が $1$ で偏角が $\dfrac{2\pi}{3},\,\dfrac{4\pi}{3}$ と $\dfrac{\pi}{3},\, -\dfrac{\pi}{3}$ となる複素数となります．このとき，新しい実数パラメータ $a$ を導入して多項式 $F_{a}(t)=t^2+at+1$ を考えると， $-1\leqq a\leqq 1$ において $F_a(t)$ の根は単位円上にのり， $F_1(t)=\varPhi_3(t)$ かつ $F_{-1}(t)=\varPhi_6(t)$ が成り立ち， $\varPhi_3(t)$ と $\varPhi_6(t)$ の $2$ つの根を単位円を通して移しています．それらの根の動きは複素平面上ちょうど下のようになります．

このように同じ次数 $n$ の円分多項式 $g_0(t),\,g_1(t)$ に対して，ある実数パラメータ $a$ をもつ実数係数 $n$ 次多項式 $G_a(t)$ が

(1) $G_{a_0}(t)=g_0(t)$ かつ $G_{a_1}(t)=g_1(t)$ を満たし

(2) $G_a(t)$ は $a_0$ と $a_1$ の間において根をすべて単位円上にもつ

とき， $G_a(t)$ を $g_0(t)$ と $g_1(t)$ の間を繋ぐ補間多項式と呼ぶことにしましょう．

先程の例において， $F_a(t)$ は $\varPhi_3(t)$ と $\varPhi_6(t)$ を間を繋ぐ補間多項式となります．実は $F_0(t)=\varPhi_4(t)$ にもなっており，すべての $2$ 次の円分多項式はこのたった $1$ つの補間多項式 $F_a(t)$ によって繋がっていることになります．

$4$ 次の円分多項式は全部で $\varPhi_5(t),\,\varPhi_8(t),\,\varPhi_{10}(t),\,\varPhi_{12}(t)$ だけあります．これらを繋ぐ補間多項式は存在するでしょうか，もし存在するならどのようにとればよいでしょうか？　複数の補間多項式によって繋いでも構いませんが， $a$ と $t$ の多項式など，なるべくシンプルな解答をお待ちしております．さらに，ほかの次数ではどうなるでしょうか？