Web日本評論 > 日評雑誌記事セレクション > 出題（2023年7月号掲載分）／応募締切（7月8日）／解答（2023年10月号掲載）

出題（2023年7月号掲載分）／応募締切（7月8日）／解答（2023年10月号掲載）

エレガントな解答をもとむ(数学セミナー)｜ 2023.06.12

『数学セミナー』のコーナー「エレガントな解答をもとむ」の出題を掲載します．奮ってご応募ください．解答・講評(3ヶ月後)は，本誌にてご確認ください．

(毎月10日頃の掲載予定)

$\def\t#1{\text{#1}}\def\dfrac#1#2{\displaystyle\frac{#1}{#2}}$

出題1

三角形に対して，その重心を中心とし 3 頂点を通る円または楕円が，ただ一つ存在することを示してください．それが楕円であるとき，その楕円率，焦点などを，三角形の楕円率，焦点などと呼ぶことにします．このとき，三角形の楕円率をその辺長，角度，面積などの諸量を用いて表してください．また余力があれば，三角形の焦点の位置を 3 頂点の位置ベクトルを用いて表してください．さらに余力があれば，焦点の作図法を考えてください．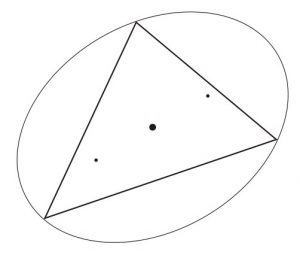

出題：山田修司 (京都産業大学理学部)

出題2

2 人のプレイヤーが次のようなゲームを行います．

石をいくつか集めてできた一つのかたまりを山と呼び，その山を $n$ 個用意します．プレイヤーは自分の手番で，以下の 2 つの操作を続けて行います． 2 人のプレイヤーが交互に操作を行い，最後に操作ができなくなったプレイヤーの負けとなります．

$k\leqq \dfrac{n}{2}$ となる正整数 $k$ を選び，$k$ 個の山を削除します．
残った $n-k$ 個の山から $k$ 個の山を選び，選んだ山をそれぞれ $2$ つの山に分割します．

$n$ 個の山からなるこのゲームの局面を $(a_1, a_2, \cdots, a_n)$ で表すことにします．各 $a_i$ は石の個数です．

例　ゲームは次のように進行します．$4$ 個の山からなるゲームの局面を $(2,3,5,8)$ とします．このとき，$k=1,\,2$ となります． 2 人のプレイヤー A と B が交互に操作を行います．

A は自分の手番で $k=1$ 個の山を選んで削除し，残った $3$ 個の山から $1$ 個の山を選び，その山を 2 つに分割します．
\begin{align*}
(2,\underline{3},5,8)\longrightarrow (2,0,5,\underline{8}) \longrightarrow (2,4,5,4)
\end{align*}

B は自分の手番で $k=2$ 個の山を選んで削除し，残った $2$ 個の山をそれぞれ 2 つの山に分割します．
\begin{align*}
(2,\underline{4},\underline{5},4)\longrightarrow (\underline{2},0,0,\underline{4})\longrightarrow (1,1,2,2)
\end{align*}

A は自分の手番で $k=2$ 個の山を選んで削除し，残った $2$ 個の山をそれぞれ 2 つの山に分割します．
\begin{align*}
(\underline{1},\underline{1},2,2)\longrightarrow (0,0,\underline{2},\underline{2})\longrightarrow (1,1,1,1)
\end{align*}

B は局面 $(1,1,1,1)$ から操作ができない (削除後に分割ができない) ため，A の勝ちとなります．

プレイヤーは常に自分の手番で最善の操作を行うと仮定する (先ほどの例の操作は最善とは限りません) とき，次の問に答えてください．