出題（2023年8月号掲載分）／応募締切（8月8日）／解答（2023年11月号掲載）
出題1
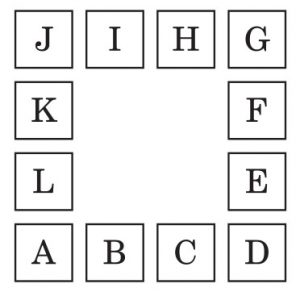
図の正方形 A, B, $\cdots$, L の中に 1 から 12 までの整数を 1 つずつ記入して，4 つの正方形が並んだ縦，横の 4 つの列に入る数の和が，いずれも 30 になるようにします．
そのような記入の仕方は全部で何通りありますか．ただし，回転や裏返しで重なり合うものも異なる記入方法とみなします．
出題：植野義明(東京大学非常勤講師)
出題2
球面上の領域で，3 つの半球面の共通部分として得られるものを球面三角形という (この場合，3 つの半球面の境界である 3 つの大円は同一点を通らないものとする)．したがって，球面三角形は 3 つの大円弧で囲まれた球面上の領域である．各大円弧を球面三角形の辺といい，その長さを球面三角形の辺の長さという．辺どうしの交点 (辺の端点) を球面三角形の頂点という．各頂点での内角とは，その頂点における辺 (大円弧) の接線どうしのなす角のことである．半径 1 の球面上の球面三角形の3辺の長さを $a,\,b,\,c$，長さ $b,\,c$ の 2 辺の交点での内角の大きさを $\alpha$ とすると，
\begin{align*}
\cos a=\cos b\cos c+\sin b\sin c\cos \alpha
\end{align*}が成立する．これは球面上の余弦定理として知られている．
問題 球面三角形 $T$ に対して，$T$ の 3 辺と同じ長さの 3 辺をもつ三角形 $\varDelta$ を平面上に描く．すると，平面上の三角形 $\varDelta$ のどの内角も球面三角形 $T$ の対応する内角よりも小さい．これを証明してください．
出題：前原濶(琉球大学名誉教授)
応募規定［解答掲載2023年11月号］
郵送の場合
B5判の用紙をご使用のうえ，解答用紙 l 枚ごとにA：出題の番号(例：8月号出題1)，B：住所，氏名(ふりがなも明記，誌上での仮名を希望される方は，こちらに明記)，年齢，職業を記入して，下記宛先までお送りください．
〒170-8474 東京都豊島区南大塚3-12-4
日本評論社 数学セミナー〈エレガントな解答をもとむ〉係
メール送信の場合
B5判のサイズで，解答用紙 1 枚ごとにA：出題の番号(例：8月号出題1)，B：住所，氏名(ふりがなも明記，誌上での仮名を希望される方は，こちらに明記)，年齢，職業を記入して，下記フォームから PDF ファイルを送信して下さい (ファイルサイズ10MBまで)．
解答記載に LaTeX ご利用の方は，テンプレートもご活用下さい．テンプレート利用は任意です．またテンプレートの漢字コードはUTF8です．ファイルが文字化けするときは適宜変換してお使いください．
投稿フォームが上手く動かないなどの場合は，susemi_elegant@nippyo.co.jp に直接お送り下さい．
注意事項
- 締切：2023年8月8日
- 二題に応募されるときは，郵送の場合は解答用紙を，メール送信の場合はファイルを，出題ごとにかえてください．
- 年齢を忘れずにお書きください．
- 解答用紙は両面の使用を不可とします．
- 解答用紙はご返却できません．
- 問題のご感想も歓迎します．
- 出題掲載号：数学セミナー2023年8月号
- 解答・講評は，本誌2023年11月号にてご確認ください．
「エレガントな解答をもとむ」をすべて見る
最新の「エレガントな解答をもとむ」はこちら