Web日本評論 > 日評雑誌記事セレクション > 出題（2023年9月号掲載分）／応募締切（9月8日）／解答（2023年12月号掲載）

出題（2023年9月号掲載分）／応募締切（9月8日）／解答（2023年12月号掲載）

エレガントな解答をもとむ(数学セミナー)｜ 2023.08.10

『数学セミナー』のコーナー「エレガントな解答をもとむ」の出題を掲載します．奮ってご応募ください．解答・講評(3ヶ月後)は，本誌にてご確認ください．

(毎月10日頃の掲載予定)

$\def\t#1{\text{#1}}\def\dfrac#1#2{\displaystyle\frac{#1}{#2}}$

出題1

一見すると，エッ本当？と思うかもしれませんが，次のような等式が成り立ちます．証明も簡単にできます．
\begin{align*}
&\sqrt{180-45\sqrt{5}} + \sqrt{86-38\sqrt{5}} = \sqrt{56+19\sqrt{5}}, \\
& \sqrt{104+48\sqrt{5}}+\sqrt{81+45\sqrt{5}} = \sqrt{389+177\sqrt{5}}.
\end{align*}

(1) $\sqrt{a+b\sqrt{5}}+\sqrt{c+d\sqrt{5}} =\sqrt{1+\sqrt{5}}$ となるような $0$ でない整数 $a$, $b$, $c$, $d$ は存在するでしょうか．

(2) $\sqrt{a+18\sqrt{5}}+\sqrt{3+4\sqrt{5}}=\sqrt{x+y\sqrt{5}}$ となるような整数 $a,\, x,\, y$ は存在するでしょうか.

(3)最初の二つの等式において，左辺のルートの中の符号をそれぞれ一か所ずつ変えると，右辺は
\begin{align*}
&\sqrt{180+45\sqrt{5}} + \sqrt{86+38\sqrt{5}} = \sqrt{476+185\sqrt{5}}, \\
& \sqrt{-104+48\sqrt{5}}+\sqrt{-81+45\sqrt{5}} = \sqrt{19+9\sqrt{5}}
\end{align*}のように再び一つのルートのかたちにまとまります．このようなことが一般に成り立つことを示してください．

(4)一番最初の等式
\begin{align*}
\sqrt{180-45\sqrt{5}} + \sqrt{86-38\sqrt{5}} = \sqrt{56+19\sqrt{5}},
\end{align*}の続きとして，左へ一つずつずらした等式
\begin{align*}
& \sqrt{86-38\sqrt{5}} + \sqrt{56+19\sqrt{5}} = \sqrt{104+7\sqrt{5}}, \\
& \sqrt{56+19\sqrt{5}} + \sqrt{104+7\sqrt{5}} = \sqrt{234+90\sqrt{5}}
\end{align*}が成り立ちます．この整数を使った等式の列は，この後も無限に続けることができるでしょうか．

一問，二問，三問だけの解答も歓迎します．

出題：阿賀岡芳夫 (広島大学名誉教授)

出題2

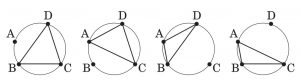
(1)円周上に 4 個の点 A, B, C, D が反時計回りに並んでいます．このとき，次の等式が成り立つことを示してください．
\begin{align*}
\t{BC} \cdot \t{CD} \cdot \t{DB} – \t{AC} \cdot \t{CD} \cdot \t{DA} + \t{AB} \cdot \t{BD} \cdot \t{DA} – \t{AB} \cdot \t{BC} \cdot \t{CA} = 0
\end{align*}

(2)円周上に $2n$ 個の点 $\t{A}_1, \t{A}_2, \cdots, \t{A}_{2n}$ が反時計回りに並んでいます．$1 \leqq k \leqq 2n$ について，
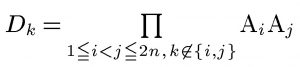と置きます．つまり，$D_k$ は，点 $\t{A}_k$ を除いた残りの $2n-1$ 点におけるすべての 2 点間の距離の積です．このとき，次の等式が成り立つことを示してください．
\begin{align*}
D_1 – D_2 + D_3 – D_4+ \cdots + D_{2n-1} – D_{2n} = 0
\end{align*}