出題（2023年10月号掲載分）／応募締切（10月8日）／解答（2024年1月号掲載）
出題1
$n$ チームが参加する大会でたくさんの試合がおこなわれる．ただし同じ相手とは 2 回以上対戦せず，またどの 4 チームをみてもその中での試合数が高々 1 のチームがある (これを「4 チーム条件」と呼ぶことにする)．
- $n=7$ のとき試合総数が 9 となる例 (対戦組合せ) をあげよ．
- 一般に試合総数は $n\sqrt n$ を超えないことを示せ．
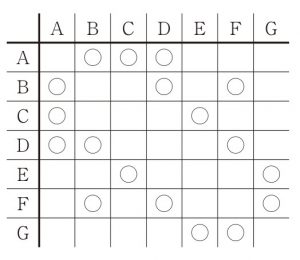
例えば $\t{A}\sim\t{G}$ の 7 チームが表のような 9 試合をおこなったとき，A, B, C, D の 4 チームをみると C はこの中で 1 試合だけである．しかし A, B, D, F の 4 チームをみるとどのチームもこの中で 2 試合以上おこなっていて「4 チーム条件」をみたさない．
$n$ チームの中の 2 チームを固定したとき，その両方と対戦するチームに注目するとよい．
出題：徳重典英（琉球大学教育学部）
注：「2」の問題文が誌面では下記のようになっていましたが，これは誤りでした．このページでも 2023 年 9 月 14 日までは同じく誤っておりました．お詫びして訂正いたします．(2023 年 9 月 14 日記)
- (誤)「一般に試合総数は $n\sqrt{n}/2$ を超えないことを示せ」
- (正)「一般に試合総数は $n\sqrt{n}$ を超えないことを示せ」
出題2
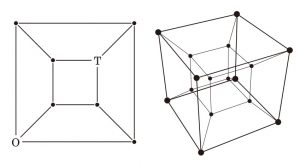
$n$-次元超立方体 $I^n$ の頂点と辺からなる図形 (グラフ) を考えます．各辺は 1 オーム ($\varOmega$) の抵抗素子でできています．原点 $\t{O}= (0, \cdots, 0)$ とその対角点 $\t{T} = (1, \cdots, 1)$ の間の抵抗を $R_n$ とします．明らかに $R_1 = 1$ で，合成抵抗の公式から $R_2 = 1$ です．
- 問1 $R_3$ と $R_4$ を求めてください．
- 問2 $R_n$ を求めてください．
さらに興味のある人は，対角点とは限らない二点間の抵抗についても考えてください．解答は問 1 だけでも良いし，問 2 だけでも十分です．
なお，自然数 $n$ に対し，$n$-次元超立方体 $I^n$ とは，$(x_1,\cdots,x_n)$ ($(x_i)$ は 0 か 1 である) の形の $2^n$ 個の点を頂点とし，成分が 1 つだけ異なる頂点同士を辺で結んでできる図形 (グラフ) のことです．とくに $n=1$ の場合は線分，$n=2$ の場合は正方形，$n=3$ の場合は立方体となります．
図1 左：立方体．頂点同士の接続関係だけを示したもの．右の図は Wikipedia の記事「超立方体」の図を改変して使用．
出題：吉田知行（北海道大学名誉教授）
応募規定［解答掲載2024年1月号］
郵送の場合
B5判の用紙をご使用のうえ，解答用紙 1 枚ごとにA：出題の番号(例：10月号出題1)，B：住所，氏名(ふりがなも明記，誌上での仮名を希望される方は，こちらに明記)，年齢，職業を記入して，下記宛先までお送りください．
〒170-8474 東京都豊島区南大塚3-12-4
日本評論社 数学セミナー〈エレガントな解答をもとむ〉係
メール送信の場合
B5判のサイズで，解答用紙 1 枚ごとにA：出題の番号(例：10月号出題1)，B：住所，氏名(ふりがなも明記，誌上での仮名を希望される方は，こちらに明記)，年齢，職業を記入して，下記フォームから PDF ファイルを送信して下さい (ファイルサイズ10MBまで)．
解答記載に LaTeX ご利用の方は，テンプレートもご活用下さい．テンプレート利用は任意です．またテンプレートの漢字コードはUTF8です．ファイルが文字化けするときは適宜変換してお使いください．
投稿フォームが上手く動かないなどの場合は，susemi_elegant@nippyo.co.jp に直接お送り下さい．
注意事項
- 締切：2023年10月8日
- 二題に応募されるときは，郵送の場合は解答用紙を，メール送信の場合はファイルを，出題ごとにかえてください．
- 年齢を忘れずにお書きください．
- 解答用紙は両面の使用を不可とします．
- 解答用紙はご返却できません．
- 問題のご感想も歓迎します．
- 出題掲載号：数学セミナー2023年10月号
- 解答・講評は，本誌2024年1月号にてご確認ください．
「エレガントな解答をもとむ」をすべて見る
最新の「エレガントな解答をもとむ」はこちら