Web日本評論 > 日評雑誌記事セレクション > 出題（2023年11月号掲載分）／応募締切（11月8日）／解答（2024年2月号掲載）

出題（2023年11月号掲載分）／応募締切（11月8日）／解答（2024年2月号掲載）

エレガントな解答をもとむ(数学セミナー)｜ 2023.10.11

『数学セミナー』のコーナー「エレガントな解答をもとむ」の出題を掲載します．奮ってご応募ください．解答・講評(3ヶ月後)は，本誌にてご確認ください．

(毎月10日頃の掲載予定)

$\def\t#1{\text{#1}}\def\dfrac#1#2{\displaystyle\frac{#1}{#2}}$

出題1

後退するときにジャンプがあるランダムウォークに関する問題です．

どの面も均等の確率で出る $m+n$ 面サイコロがあり，$m$ 面には黒字で1が記され，残りの $n$ 面には赤字で，いずれも 1 より大きい整数 $a_1,\cdots,a_n$ がそれぞれ記されています．数直線の原点を出発点とし，このサイコロを振って黒字の面が出たら右に 1 進み，赤字の面が出たら，その面に書かれた数のぶんだけ左に進む，ということをずっと続けます．このとき，「いつか原点よりも左に行く」ということが起きる確率はいくらでしょうか．

実は，$a_1+\cdots +a_n\geqq m$ の場合には確率は 1 となり，その議論をしてもらうのも煩雑なので，解答は $a_1+\cdots +a_n<m$ の場合に限定してもらってかまいません．また，本問のままでは難しいときには，もう少し特定の場合，たとえば赤字の整数がすべて同じ場合や，さらに特定して，たとえば 18 面が黒字の 1 で，残りの 2 面が赤字の 5 である 20 面のサイコロといった場合のみについて解いた答案の提出も歓迎します．

出題：岩沢宏和（パズル研究家）

出題2

${}_n \t{C}_k$ が $2$ で何回割り切れるかについて考えてみる．正の整数 $a$ に対して，$a$ が $2$ で割り切れる回数を $v (a)$ と定める．例えば，$v (1) = v (3) = 0,\, v (2) = 1,\, v (100) = 2$ となる．整数 $n\geqq 0$ に対して $f (n) = \max\{v ({}_n \t{C}_k) \mid 0\leqq k \leqq n\}$ と定める．$n$ が非負の偶数を動くとき，
\begin{align*}
2^{f (n)} + \sum_{k=0}^{n} (-1)^k v ({}_n \t{C}_k)
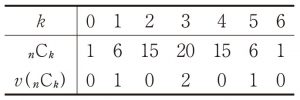
\end{align*}の最大値を求め，最大値になるような $n$ の必要十分条件を与えよ．例えば $n=6$ の場合，${}_n \t{C}_k,\, v ({}_n \t{C}_k)$は表 1 のようになるので，$f (6) = 2$ で
\begin{align*}
2^{f (6)} + \sum_{k=0}^{6} (-1)^k v ({}_6 \t{C}_k)& = 2^2 + (-1 -2 -1) \\
&= 0
\end{align*}となる．