出題(2024年1月号掲載分)/応募締切(1月8日)/解答(2024年4月号掲載)
出題1
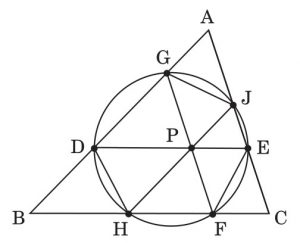
△ABC の内部に一点 P をとり,P を通って 3 辺 BC,CA,AB に平行な線を引き,それらが辺と交わる点を順次 D,E;F,G;H,J とします (図参照).
ここでこれらの 6 点 D,H,F,E,J,G が同一の円周上に載るための,点 P の位置に関する必要十分条件を,ベクトルなどを活用して,表現してください.
付記 この点 P は,いわゆる三角形の「五心」の内には入りませんが,それらに続く重要な点であり,いろいろの名があります.余裕があれば,そのとき 3 本の小線分 GJ,DH,EF の長さが相等しいことを示し,それらの共通の長さを,3 辺長 a=BC,b=CA,c=AB によって表してください.
出題:一松 信 (京都大学名誉教授)
出題2
自然数 m,n に対して,累乗の和
Sm(n)=n∑k=1km=1m+2m+⋯+nmについての問題です.m=1,2,3 については
S1(n)=n∑k=1k=12n(n+1)S2(n)=n∑k=1k2=16n(n+1)(2n+1)S3(n)=n∑k=1k3={12n(n+1)}2という公式が,高校の教科書にも載っています.これらの公式を見て,
「あっ,S1(n) の二乗は S3(n) に等しいんだ」
と思った人も多いはずですね.では,これ以外に,
累乗すると,2 つの公式が等しくなる場合,
すなわち,すべての自然数 n について
Sp(n)a=Sq(n)bが成り立つ自然数 p,q,a,b (p<q) があるでしょうか? 調べてみてください.
累乗の和の公式は,なじみのある話題ですので,『数学セミナー』の賢明な読者の皆さんには,やさしい問題でしょうか? 「エレガントでない長い解答」を「エレファントな解答」という,古くからの表現がありますが,それに対抗して言うと,「ビビッ」とくる「エレキテルな解答」をお待ちしています.

出題:中内伸光 (山口大学大学院創成科学研究科)
応募規定[解答掲載2024年4月号]
郵送の場合
B5判の用紙をご使用のうえ,解答用紙 1 枚ごとにA:出題の番号(例:1月号出題1),B:住所,氏名(ふりがなも明記,誌上での仮名を希望される方は,こちらに明記),年齢,職業を記入して,下記宛先までお送りください.
〒170-8474 東京都豊島区南大塚3-12-4
日本評論社 数学セミナー〈エレガントな解答をもとむ〉係
メール送信の場合
B5判のサイズで,解答用紙 1 枚ごとにA:出題の番号(例:1月号出題1),B:住所,氏名(ふりがなも明記,誌上での仮名を希望される方は,こちらに明記),年齢,職業を記入して,下記フォームから PDF ファイルを送信して下さい (ファイルサイズ10MBまで).
解答記載に LaTeX ご利用の方は,テンプレートもご活用下さい.テンプレート利用は任意です.またテンプレートの漢字コードはUTF8です.ファイルが文字化けするときは適宜変換してお使いください.
(1)投稿フォームが上手く動かない,(2)受信確認メール希望の方でメールが届かない,などの場合,susemi_elegant@nippyo.co.jp に直接お送り下さい.
注意事項
- 締切:2024年1月8日
- 二題に応募されるときは,郵送の場合は解答用紙を,メール送信の場合はファイルを,出題ごとにかえてください.
- 年齢を忘れずにお書きください.
- 解答用紙は両面の使用を不可とします.
- 解答用紙はご返却できません.
- 問題のご感想も歓迎します.
- 出題掲載号:数学セミナー2024年1月号
- 解答・講評は,本誌2024年4月号にてご確認ください.
「エレガントな解答をもとむ」をすべて見る
最新の「エレガントな解答をもとむ」はこちら





