出題(2018年12月号掲載分)/応募締切(12月8日)/解答(2019年3月号掲載)
出題1
A さんと B さんは,コイントスで勝負を決めることにした.ところが手元にあるコインは,どう見ても歪んでいて,公平な勝負ができそうにない.そこで A さんは,次の方法を考案した.まず,コインを 2 回投げる.表,裏の順に出たら A さんの勝ち,裏,表の順に出たら B さんの勝ちとしよう.表,表が出たり,裏,裏が出たらやり直しだ.
問題 1 この歪んだコインの表が出る確率を $p$ としたとき,勝負がつくまでにコインを投げる回数の期待値はどのくらいだろうか.期待値が最も小さくなる $p$ の値と,期待値の最小値も求めてもらいたい.
問題 2 B さんは,上記の方法よりもコインを投げる回数の期待値が少ない方法を思い付いた.さてそれは,どんな方法だろうか.この方法での期待値が最も小さくなる $p$ の値と,期待値の最小値も求めてもらいたい.
問題 2 の答えは,いろいろと考えられるが,上記の期待値の最小値が小さいほど良いものとしよう.
出題:上原隆平
出題2
$n$ 個の頂点と $n-1$ 個の辺を持つ以下のような図形を考える.

各頂点 $\alpha_1,\cdots,\alpha_n$ に,それぞれ実数 $\lambda_1,\cdots,\lambda_n$ が書き込まれた状態を考える.状態を変化させる $n$ 種類の操作 $s_1,\cdots,s_n$ を以下のように定める:
● $k = 1,\cdots, n$ を固定する.頂点 $\alpha_k$ と辺で結ばれているすべての頂点に対し,その頂点に書き込まれた数に $\lambda_k$ を足す.またその後,$\alpha_k$ に書き込まれている $\lambda_k$ を $-1$ 倍する.この一連の操作を “頂点 $\alpha_k$ に対応する操作 $s_k$” と呼ぶ.
次図は $n = 4$ における操作 $s_2$ の例である:
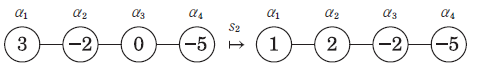
次のような一人用のゲームを考える:与えられた初期状態から出発して,プレイヤーは「頂点を一つ選び,その頂点に対応する操作を施す」という手順を繰り返す.各頂点に書き込まれている数がすべて非負になったらゴール.
問 1 どういう初期状態から出発しても,うまく手順をこなせば必ずゴールできることを示せ.
問 2 同じ初期状態から出発すると,どういう手順でゴールしても,最終的な状態は同じものになってしまうことを示せ.
問 3 左右対称,つまり “すべての $i=1,\cdots,n$ について $\lambda_i=\lambda_{n+1-i}$” となる初期状態から出発すると,ゴール時にも必ず左右対称な状態となることを示せ.
一部だけの解答も歓迎します.
出題:奥田隆幸
応募規定[解答掲載2019年3月号]
郵送の場合
B5版の用紙をご使用のうえ,解答用紙 l 枚ごとにA:問題の番号(例:12月号問1),B:住所,氏名(ふりがなも明記,誌上での仮名を希望される方は,こちらに明記),年齢,職業を記入して,下記宛先までお送りください.
〒170-8474 東京都豊島区南大塚3-12-4
日本評論社 数学セミナー〈エレガントな解答をもとむ〉係
メール送信の場合
B5版のサイズで,解答用紙 l 枚ごとにA:問題の番号(例:12月号問1),B:住所,氏名(ふりがなも明記,誌上での仮名を希望される方は,こちらに明記),年齢,職業を記入して,下記フォームから PDF ファイルを送信して下さい.
解答記載に LaTeX ご利用の方は,テンプレートもご活用下さい.テンプレート利用は任意です.またテンプレートの漢字コードはUTF8です.ファイルが文字化けするときは適宜変換してお使いください.
投稿フォームが上手く動かないなどの場合は,susemi_elegant@nippyo.co.jp に直接お送り下さい.
注意事項
- 締切:2018年12月8日
- 2 問に応募されるときは,郵送の場合は解答用紙を,メール送信の場合はファイルを,問題ごとにかえてください.
- 年齢を忘れずにお書きください.
- 解答用紙は両面の使用を不可とします.
- 解答用紙はご返却できません.
- 問題のご感想も歓迎します.
- 出題掲載号:数学セミナー2018年12月号.
- 解答・講評は,本誌2019年3月号にてご確認ください.





