出題(2019年4月号掲載分)/応募締切(4月8日)/解答(2019年7月号掲載)
出題1
3 と 5 や,11 と 13 のように差が 2 である素数の組を双子素数といいますが,これの複素数版を考えます.
複素数 z=x+iy で,実部 x と虚部 y が整数であるものをガウス整数といいます.また,0,±1,±i を除くガウス整数 z のうち,次の性質をみたすものをガウス素数といいます.
z=αβ と,z が二つのガウス整数 α,β の積に分解されるとき,|α| と |β| のいずれかが 1 に等しい.
このとき,ガウス整数 z のうち,
z+1,z−1,z+i,z−iがすべてガウス素数のものを考えます.そのような z は,
3±i,−3±i,1±3i,−1±3i,2±2i,−2±2iの 12 個を除くと,かならず実部と虚部が共に 5 の倍数となることを示してください.
出題:濵中裕明
出題2
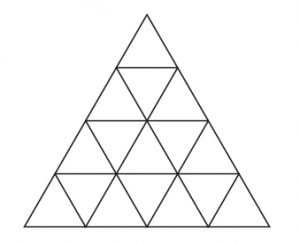
図 1 のように正三角形が並んでいる図形を n 段の三角格子とよぶ.ただし,n は外側の各辺に並んでいる正三角形の数である.
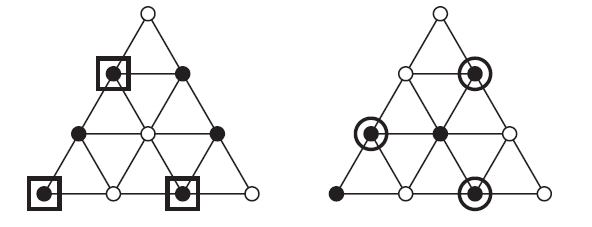
三角格子の頂点を何色かで塗り,3 頂点がすべて同じ色の正三角形(単色三角形とよぶ)を見つけたい.ただし,単色三角形はいくつかの小三角形を貼り合わせた正三角形のなかから探す.向きは上向きでも下向きでも構わないとする.例えば図 2 (左)には四角で囲った 3 点を頂点とする単色三角形が存在するが,(右)の丸で囲った 3 点は単色三角形を構成せず,実際に単色三角形が存在しない塗り方となっている.
(1) 4 段の三角格子は,頂点をどのように 2 色で塗っても単色三角形を持つことを示せ.
(2) 5 段の三角格子の 3 色での頂点の塗り方で,単色三角形を持たないものを一つ示せ.
(3) 10000 段の三角格子は頂点をどのように 3 色で塗っても単色三角形を持つことを示せ.
なお,(3)はもっと大きな三角格子で考えても構わない.少々大きくとも,より簡潔な議論を期待する.また,(1)や(2)のみの解答も歓迎する.
出題:小関健太
応募規定[解答掲載2019年7月号]
郵送の場合
B5版の用紙をご使用のうえ,解答用紙 l 枚ごとにA:問題の番号(例:4月号問1),B:住所,氏名(ふりがなも明記,誌上での仮名を希望される方は,こちらに明記),年齢,職業を記入して,下記宛先までお送りください.
〒170-8474 東京都豊島区南大塚3-12-4
日本評論社 数学セミナー〈エレガントな解答をもとむ〉係
メール送信の場合
B5版のサイズで,解答用紙 l 枚ごとにA:問題の番号(例:4月号問1),B:住所,氏名(ふりがなも明記,誌上での仮名を希望される方は,こちらに明記),年齢,職業を記入して,下記フォームから PDF ファイルを送信して下さい.
解答記載に LaTeX ご利用の方は,テンプレートもご活用下さい.テンプレート利用は任意です.またテンプレートの漢字コードはUTF8です.ファイルが文字化けするときは適宜変換してお使いください.
投稿フォームが上手く動かないなどの場合は,susemi_elegant@nippyo.co.jp に直接お送り下さい.
注意事項
- 締切:2019年4月8日
- 2 問に応募されるときは,郵送の場合は解答用紙を,メール送信の場合はファイルを,問題ごとにかえてください.
- 年齢を忘れずにお書きください.
- 解答用紙は両面の使用を不可とします.
- 解答用紙はご返却できません.
- 問題のご感想も歓迎します.
- 出題掲載号:数学セミナー2019年4月号
- 解答・講評は,本誌2019年7月号にてご確認ください.