出題(2019年8月号掲載分)/応募締切(8月8日)/解答(2019年11月号掲載)
出題1
正の整数 $q$ と整数 $a,\, b$ に対して $a$ および $b$ を $q$ で割った余りが等しいとき $a\equiv b\ (\text{mod}\,q)$ と表します.
問題 2 以上の自然数 $m$ が 3 と互いに素であるとする.自然数 $k$ に対して
\begin{align*}
(m^k)^2+m^k+1
\end{align*}は素数であるとし,これを $p$ とおく.このとき,
\begin{align*}
m^{m^k+1}\equiv 1\quad (\text{mod}\,p)
\end{align*}が成立することを証明せよ.
例えば,$m=2$ で $k =1,\,3,\,9$ とすると,$(m^k)^2+m^k+1$ の値はそれぞれ 7, 73, 262657 となり,これらの値はすべて素数です.
\begin{align*}
&2^{2+1}\equiv 1\quad (\text{mod}\,7),\\
&2^{2^3+1}\equiv 1\quad (\text{mod}\, 73),\\
&2^{2^9+1}\equiv 1\quad (\text{mod}\, 262657)
\end{align*}が成立しています.これらの例から,条件が成り立つ $k$ の値を予想してみるとよいでしょう.
出題:中川暢夫+小田文仁
出題2
以下の問題は,私の勘違いで間違った解答を書いてしまった 2014 年 9 月号の出題に加筆したものです.カードの枚数を減らしましたが,賢者の思考に追いつくのはたやすくありません.再度挑戦していただけるでしょうか?
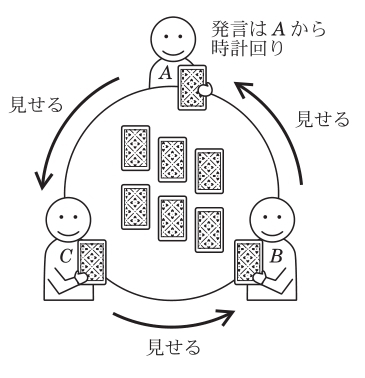
3 人の賢者 $A,\, B,\, C$ がカード遊びをしています.1 から $N =9$ までの数が書かれた $N$ 枚のカードが円卓上に裏向きに置いてあり,賢者たちは 1 枚ずつ手元に取ります.大小比較で中間の数を取った賢者が勝ちます.でも,一斉にカードをオープンするだけでは脳がへたれるので,次のようにしました.賢者たちは取ったカードを見たあと,自分の右隣りにも見せます.そして $A$ から順に時計回りに,勝敗について確定したこと,つまり「誰の勝ち」あるいは勝者が決まらないときは「誰の負け」と発言します.勝敗に関する新しい確定情報がないときはニッコリ会釈するだけです.
最初からニッコリが連続したあと,ある賢者が「わしの勝ちぢゃな.最初からのニッコリがこれより長く連続することはなかろうて」と言いました.誰がどのようなカードの組合せで勝ったのでしょうか?
可能なら,最長のニッコリが続いたあと,発言者が勝つと宣言できるカードの組合せが $N =9$ のときと同じ個数しかない次の $N\ (> 9)$ を求めてください.
出題:竹内郁雄
応募規定[解答掲載2019年11月号]
郵送の場合
B5版の用紙をご使用のうえ,解答用紙 l 枚ごとにA:出題の番号(例:8月号出題1),B:住所,氏名(ふりがなも明記,誌上での仮名を希望される方は,こちらに明記),年齢,職業を記入して,下記宛先までお送りください.
〒170-8474 東京都豊島区南大塚3-12-4
日本評論社 数学セミナー〈エレガントな解答をもとむ〉係
メール送信の場合
B5版のサイズで,解答用紙 l 枚ごとにA:出題の番号(例:8月号出題1),B:住所,氏名(ふりがなも明記,誌上での仮名を希望される方は,こちらに明記),年齢,職業を記入して,下記フォームから PDF ファイルを送信して下さい.
解答記載に LaTeX ご利用の方は,テンプレートもご活用下さい.テンプレート利用は任意です.またテンプレートの漢字コードはUTF8です.ファイルが文字化けするときは適宜変換してお使いください.
投稿フォームが上手く動かないなどの場合は,susemi_elegant@nippyo.co.jp に直接お送り下さい.
注意事項
- 締切:2019年8月8日
- 二題に応募されるときは,郵送の場合は解答用紙を,メール送信の場合はファイルを,出題ごとにかえてください.
- 年齢を忘れずにお書きください.
- 解答用紙は両面の使用を不可とします.
- 解答用紙はご返却できません.
- 問題のご感想も歓迎します.
- 出題掲載号:数学セミナー2019年8月号
- 解答・講評は,本誌2019年11月号にてご確認ください.





