出題(2020年7月号掲載分)/応募締切(7月8日)/解答(2020年10月号掲載)
出題1
集合$\varLambda=\{1, 2, 3, 4, 5, 6, 7\}$ の三つの要素を各行に並べた次の表
\begin{align*}
&1,\, 2,\, 4\\
&2,\, 3,\, 5\\
&3,\, 4,\, 6\\
&4,\, 5,\, 7\\
&5,\, 6,\, 1\\
&6,\, 7,\, 2\\
&7,\, 1,\, 3
\end{align*}は,「$\varLambda$ の任意の異なる二つの要素 $i,\,j$ に対して,$i$ と $j$ を両方含む行がただ一つ存在する」という性質を持ちます.
問題 (1) $n$ を $5$ より大きい自然数とします.集合 $\varOmega=\{1,2,\cdots,3n\}$ の $n$ 個の要素を各行に並べた表
\begin{align*}
&B_1\\
&B_2\\
&\ \vdots\\
&B_{r(n)}
\end{align*}が下記の条件($\bigstar$)を満たすとします.
$\varOmega$ の任意の異なる五つの要素に対して,それらすべてを含む行がただ一つ存在する.($\bigstar$)
このとき $n$ は二つの値に限定されます.これらの $n$ の値と各 $n$ に対する表の行数 $r(n)$ を求めてください.
(2) (1)で求めた二つの $n$ の値の大きい方について,($\bigstar$)を満たす上記の表の一つの行 $B$ を固定して考えます.$i=0,1,\cdots, n$ なる各 $i$ に対して,$|B\cap P|=i$ を満たす行 $P$ の総数 $m(i)$ を求めてください($|B\cap P|$ は行 $B$ と $P$ の両方に含まれる要素の個数です).
出題:中川暢夫
出題2
平面上で,互いに素な自然数を座標にもつ点の集合
\begin{align*}
C=\{(a,b)\in\mathbb N\times\mathbb N\,|\,\text{gcd}(a,b)=1\}
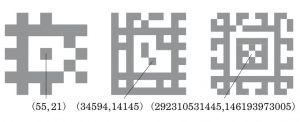
\end{align*}を考えます.縦横斜めで接している(すなわち $x$ 座標 $y$ 座標とも差が $1$ 以下の) $C$ の点を辿って行けるという連結関係で,$C$ を連結成分に分けます.点 $(1,1)$ を含む連結成分を大陸と呼び,そうでない連結成分を島と呼び,島に含まれる点の個数を島の面積ということにします.下図に面積 $1,\, 3,\, 20$ の島の例を示します.
このとき,次のことを示してください.
(1) 面積が無限の島は存在しない
(2) 面積 $1$ の島が無数に存在する
(3) いくらでも大きい面積の島が存在する
(3)が難しければ(1),(2)だけでも結構です.中国剰余定理などの初等的な事実は,主張をきちんと述べれば証明する必要はありません.ディリクレの算術級数定理などの少し高度な事実も証明なしに用いて構いませんが,用いないで済めばその方が良しとします.
出題:山田修司
応募規定[解答掲載2020年10月号]
郵送の場合
B5判の用紙をご使用のうえ,解答用紙 l 枚ごとにA:出題の番号(例:7月号出題1),B:住所,氏名(ふりがなも明記,誌上での仮名を希望される方は,こちらに明記),年齢,職業を記入して,下記宛先までお送りください.
〒170-8474 東京都豊島区南大塚3-12-4
日本評論社 数学セミナー〈エレガントな解答をもとむ〉係
メール送信の場合
B5判のサイズで,解答用紙l枚ごとにA:出題の番号(例:7月号出題1),B:住所,氏名(ふりがなも明記,誌上での仮名を希望される方は,こちらに明記),年齢,職業を記入して,下記フォームから PDF ファイルを送信して下さい(ファイルサイズ10MBまで).
解答記載に LaTeX ご利用の方は,テンプレートもご活用下さい.テンプレート利用は任意です.またテンプレートの漢字コードはUTF8です.ファイルが文字化けするときは適宜変換してお使いください.
投稿フォームが上手く動かないなどの場合は,susemi_elegant@nippyo.co.jp に直接お送り下さい.
注意事項
- 締切:2020年7月8日
- 二題に応募されるときは,郵送の場合は解答用紙を,メール送信の場合はファイルを,出題ごとにかえてください.
- 年齢を忘れずにお書きください.
- 解答用紙は両面の使用を不可とします.
- 解答用紙はご返却できません.
- 問題のご感想も歓迎します.
- 出題掲載号:数学セミナー2020年7月号
- 解答・講評は,本誌2020年10月号にてご確認ください.





