単位の授業 — 小学校ではどう教えられているか?(石原清貴)
 私たちの日常生活と密接不可分な「単位」.この小特集では,(1)
私たちの日常生活と密接不可分な「単位」.この小特集では,(1)1.単位の指導の変遷
算数における量と単位の指導法の変遷は,大雑把に 3 つの時期に分けることができます.
はじめの時期は,戦後から平成に至る期間で,主に計測機器を使った計測中心の時期です.
次にやってくるのが,昭和の終わりから現在に至る「量と単位の 4 段階指導」がメインとなった時期です.この「量と単位の 4 段階指導」は,遠山啓が提案し,民間の教育団体である数学教育協議会 (略称:数教協) が実証的に発展させてきた指導法です.この指導法は一時期,広く現場に受け入れられ,現在でも教科書に取り入れられています (ただ,かなり形骸化している).
そして最後が,学力テスト以降の教科書&プリント学習中心の指導法の時期です.この現在進行形の指導方法が今回の話題のメインになります.
2.計器を使った測定中心主義の時代
この指導方法は別に戦後始まったわけではなく,明治から戦後にかけて一貫して行われてきた “道具ありき” の指導法で,物差しや巻き尺,あるいは秤や天秤,あるいは桝,あるいは時計で,それぞれの道具の使い方を通して単位や換算を学ぶというスタイルです.この方法はそれなりに楽しい方法で,物差しや台上ばかり, $\t{L}$ 桝や $\t{dL}$ 桝は算数教材室にたくさん用意されていて,一人一人もしくはグループで使えるようになっていました.その他に $1\t{cm}^3$ 立方体もたくさんあり,面積や体積の勉強でも使えるようにそろえてありました (理科・数学教育振興法 (1953) のおかげ).子どもたちはこれらの計量道具を使った計測を通して量感を身につけ,単位に慣れ親しむことができました.
また, 1955 年 (昭和 30 年) から 1975 年 (昭和 50 年) にかけては,まだまだ身の回りに量り売りの商品がたくさんありましたし,生活の場面で長さや重さ,嵩を測ることは決して珍しいものではありませんでした.その意味では生活体験と直結していたのです.
残念ながら,いまの子どもたちは,物の量を量る現場に出くわす機会が極端に減っています.そのうえ計測機器もデジタル化されていて,しくみが理解できなくなっています.だからこそ丁寧な量と単位の指導が必要なのです.
3.「量と単位の 4 段階指導法」の時代
前に書いたとおり,1952 年,遠山啓・銀林浩によって提唱された量と単位の指導法は,それまでの計測中心の指導に対して,「量の認識は多い・少ないという比較を通して認知されるという前提から,単位の成り立ちをつかませることが必要だ」という考えのもと提案された指導法です.
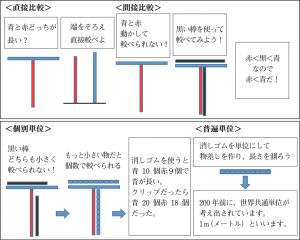
遠山・銀林は,普遍単位に至る指導過程を次の 4 段階で示しており,これを「量と単位の 4 段階指導」と呼んでいます.
- 第 1 段階は,$A$ と $B$ 2 つの量を直接比べて,どちらが大きいかを決める段階.[直接比較]
- 第 2 段階は,$A$ と $B$ の 2 つの量を直接比べられないときには,仲介物 $C$ を使って比べ, $A<C,\,C< B$ なので $A<B$ とする段階.[間接比較]
- 第 3 段階は,$A$ と $B$ を個数で表すことのできる物 $D$ を用いて,$D$ の個数で比べる段階.この段階で物 $D$ は単位となる.[個別単位] (任意単位と呼ぶこともある)
- 第 4 段階は,世界共通の単位で量を表す段階.[普遍単位]
図示すると次のようになります。
1992 年 (平成 4 年) の算数の学習指導要領から,「直接比較」とか「身近な物を単位として」という言葉が見られるようになり,量と単位の 4 段階指導が本格的に取り入れられるようになりました.この時期の算数指導の解説書では頻繁に 4 段階指導について言及されるようになり,量と単位の 4 段階指導が公に認められたのです.また,当時の「新学力観」の中に示された体験重視の指導法に量の 4 段階指導法がぴったりだったこともあり,この指導法は全国各地の小学校で実践されるようになりました (もちろんすべての教員がこういった指導法で授業したというわけではありません).
この当時の指導をちょっと覗いてみましょう.
2 年生算数 — 長さの授業
《誰の蛇が長いかな? 》
子どもたち一人一人に同じ量の油粘土を渡し,そこからできるだけ長い蛇を作らせます.そして,次のように聞きます.
そう問いかけると,隣どうしですぐ比べられる子もいるけれども,全員の長さを比較するのが困難であることに気付きます.
「みんなの作ったヘビの端をそろえて並べたらいい」
という意見が出てきますが,残念ながら粘土を細く延ばしたヘビ君は,運ぼうとすればちぎれてしまいます.ひもを使って比べたり手の幅で比べたりしても,誰が一番長いかは分かりません.そうこうしているうちに,
「手の幅いくつ分で測ったらいい」
というアイデアが出てきます.実際に一人一人が測って,手の幅いくつ分という数値が出るのですが,残念ながら手の幅が一人一人違うので,比べることができません.
「何か同じ大きさの物で比べられないかな? 」
と投げかけると,
といってきます.
「積み木だったらみんな同じだから,比べられるよね」
そういって積み木をたくさん持ってきて,子どもたちが自分で作ったヘビ君の横に積み木を並べていきます.
「僕は積み木 $12$ 個分」「私は積み木 $15$ 個分」
という声があちこちから聞こえてきます.
「そうだね.これだったら誰のヘビ君が一番長いか,わかるね」
こうやって個別単位を作って較べる体験をします.
そのあと「積み木物差し」を作り,いろいろな物の長さを測るのですが,この「積み木物差し」は教室の中でしか通用しません.そこで,世界中で通用する物差し「メートル物差し」を教えるわけです.
たかが長さを教えるのに,こんなことまでやる必要があるのかと,疑問に思われるかもしれません.しかし,単に単位を教え,測り方を教え,量に関係する問題を解くのではなく,量をどうやって比較するのか考え,数値化すると比較できるのだと気付く体験は,計量の文化を理解する貴重な算数体験です.このような活動は,その後「算数的活動」という大きな枠の中で捉えられるようになります.
 石原清貴(いしはら・きよたか)
石原清貴(いしはら・きよたか)1954 年生まれ 香川県志度町出身 (現さぬき市) 元小学校教員・退職後「算数クリニック・石原算数教育研究所」を開設,算数数学で躓いた子どもたちのフォローをしたり youtube (石原清貴チャンネル) で算数教育法の動画配信を行ったりしている.
著書『算数を探しに行こう!--- 式」や「計算」のしくみがわかる五つの物語』(新潮社)・『算数少女ミカ 割合なんてこわくない』(日本評論社),『まるごと算数授業』(喜楽研) 監修など.