出題(2020年11月号掲載分)/応募締切(11月8日)/解答(2021年2月号掲載)
出題1
$\triangle\t{A}_0\t{B}_0\t{C}_0$ を平面 $\varPi$ 上の正三角形,$\varGamma$ をその外接円とします.$\triangle\t{ABC}$ を正三角形でない任意の三角形とします.このとき,平面 $\varPi$ 上の点 $\t{P}$ で以下の条件「$\triangle\t{ABC}$ を相似拡大して得られる三角形 $\triangle\t{A}’\t{B}’\t{C}’$ で,辺 $\t{B}’\t{C}’,\,\t{C}’\t{A}’,\,\t{A}’\t{B}’$ の長さが $\t{PA}_0,\,\t{PB}_0,\,\t{PC}_0$ の長さと順に等しくなるものが存在する」をみたすものがただ二つ,$\varGamma$ の内側,外側に一つずつ存在します.これを証明してください.
余裕のある方には,点 (二点) の性質や三次元への拡張など,自由に発展させて考えてみることを期待します.
出題:今井 淳
出題2
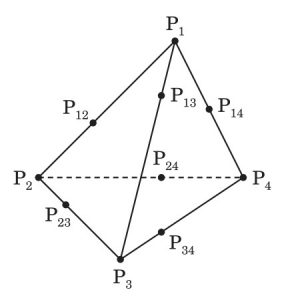
3 次元空間内に $\t P_1,\,\t P_2,\,\t P_3,\,\t P_4$ を頂点とする四面体が与えられている.各 $1\leqq i<j\leqq 4$ に対して辺 $\t P_i\t P_j$ 上に点 $\t P_{ij}$ を勝手に選ぶ.ただし以上の 10 点はすべて異なるものとする (図参照).$\t P_i$ を通る辺上に選んだ 3 点および $\t P_i$ を通る球面を $S_i$ とする.例えば $S_2$ は $\t P_{12},\,\t P_{23},\,\t P_{24}$ および $\t P_{2}$ を通る.このとき次のことを示せ.
(i) 3 個の球面 $S_1,\,S_2,\,S_3$ を平面 $\t P_1\t P_2\t P_3$ で切断して得られる 3 個の円は一点で交わる.
(ii) 4 個の球面 $S_1,\,S_2,\,S_3,\,S_4$ は一点で交わる.
出題:徳重典英
応募規定[解答掲載2021年2月号]
郵送の場合
B5判の用紙をご使用のうえ,解答用紙 l 枚ごとにA:出題の番号(例:11月号出題1),B:住所,氏名(ふりがなも明記,誌上での仮名を希望される方は,こちらに明記),年齢,職業を記入して,下記宛先までお送りください.
〒170-8474 東京都豊島区南大塚3-12-4
日本評論社 数学セミナー〈エレガントな解答をもとむ〉係
メール送信の場合
B5判のサイズで,解答用紙l枚ごとにA:出題の番号(例:11月号出題1),B:住所,氏名(ふりがなも明記,誌上での仮名を希望される方は,こちらに明記),年齢,職業を記入して,下記フォームから PDF ファイルを送信して下さい(ファイルサイズ10MBまで).
解答記載に LaTeX ご利用の方は,テンプレートもご活用下さい.テンプレート利用は任意です.またテンプレートの漢字コードはUTF8です.ファイルが文字化けするときは適宜変換してお使いください.
投稿フォームが上手く動かないなどの場合は,susemi_elegant@nippyo.co.jp に直接お送り下さい.
注意事項
- 締切:2020年11月8日
- 二題に応募されるときは,郵送の場合は解答用紙を,メール送信の場合はファイルを,出題ごとにかえてください.
- 年齢を忘れずにお書きください.
- 解答用紙は両面の使用を不可とします.
- 解答用紙はご返却できません.
- 問題のご感想も歓迎します.
- 出題掲載号:数学セミナー2020年11月号
- 解答・講評は,本誌2021年2月号にてご確認ください.





