出題(2021年1月号掲載分)/応募締切(1月8日)/解答(2021年4月号掲載)
出題1
有名なケーキカット問題であるが,ここでは公平にカットするのではなく,偏ったカットを扱う.ケーキは一様な直方体のものを考えていただけばいいだろう.太郎と花子による次のプロトコルを考える.
- 太郎がケーキを切って A と B に分ける.
- 再び太郎が A を切って A1 と A2 に分ける.
- 花子は (i) A1 を取る,または (ii) A2 を取る,または (iii) 何も取らない.
- 花子が (i) または (ii) を選択したら太郎は取られなかった方と B を取る (ゲーム終了).(iii) を選択したら太郎は A1 または A2 を取る.花子は残りを取って,B を 2 つに切る (B1,B2).
- 太郎が B1 または B2 を取り,花子が残りを取る (ゲーム終了).
(1) お互いにできるだけ多く取るために最善を尽くすと,太郎の取り分はどのくらいになるか.
(2) ステップ 1 と 2 両方を以下のように変更するとどうか.いずれも最適性に言及すること.
- 花子がケーキを切って A と B に分ける.
- 太郎はどちらかを取るか,いずれも取らない.取れば花子は残りを取ってゲーム終了.取らない場合,太郎が A を切って A1 と A2 に分ける.
出題:岩間一雄
出題2
平面上の点列 A0,A1,A2,⋯ を {An} と書くことにします.M=(mij) を 3 次正則行列(逆行列をもつ行列) であるとし,3 つの点列 {An},{Bn},{Cn} が M の成分を係数とするような線形の連立漸化式を満たすとは,
{An+1=m11An+m12Bn+m13CnBn+1=m21An+m22Bn+m23CnCn+1=m31An+m32Bn+m33Cnであることを意味するものとします (演算は座標成分ごとに行うものとします).また,たとえば点列 {An} が An+1=An で与えられたとするとき,これを自明な漸化式と呼ぶことにします.
問1 以下の条件を満たす,自明な漸化式を含まないような 3 次正則行列 M の例をできるだけたくさん見つけてください.
(条件) A0,B0,C0 が平面上の相異なる 3 点であるとしたとき,M の成分を係数とする線形の連立漸化式から決まる点列 {An},{Bn},{Cn} について,limn→∞An,limn→∞Bn,limn→∞Cn は相異なる 3 点に収束し,その極限をそれぞれ A∞,B∞,C∞ と置いたときに B∞ は A∞C∞ の中点である.
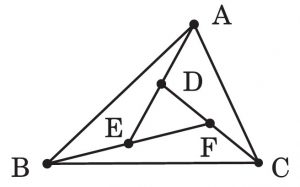
問2 自明な漸化式を含まないような,正則行列を係数とする線形の連立漸化式であって,任意の相異なる 6 点から始めて下図を得るような漸化式を提案してください.ただし,D,E,F はそれぞれ AE,BF,CD の中点であるものとします.
出題:阿原一志
応募規定[解答掲載2021年4月号]
郵送の場合
B5判の用紙をご使用のうえ,解答用紙 l 枚ごとにA:出題の番号(例:1月号出題1),B:住所,氏名(ふりがなも明記,誌上での仮名を希望される方は,こちらに明記),年齢,職業を記入して,下記宛先までお送りください.
〒170-8474 東京都豊島区南大塚3-12-4
日本評論社 数学セミナー〈エレガントな解答をもとむ〉係
メール送信の場合
B5判のサイズで,解答用紙l枚ごとにA:出題の番号(例:1月号出題1),B:住所,氏名(ふりがなも明記,誌上での仮名を希望される方は,こちらに明記),年齢,職業を記入して,下記フォームから PDF ファイルを送信して下さい (ファイルサイズ10MBまで).
解答記載に LaTeX ご利用の方は,テンプレートもご活用下さい.テンプレート利用は任意です.またテンプレートの漢字コードはUTF8です.ファイルが文字化けするときは適宜変換してお使いください.
投稿フォームが上手く動かないなどの場合は,susemi_elegant@nippyo.co.jp に直接お送り下さい.
注意事項
- 締切:2021年1月8日
- 二題に応募されるときは,郵送の場合は解答用紙を,メール送信の場合はファイルを,出題ごとにかえてください.
- 年齢を忘れずにお書きください.
- 解答用紙は両面の使用を不可とします.
- 解答用紙はご返却できません.
- 問題のご感想も歓迎します.
- 出題掲載号:数学セミナー2021年1月号
- 解答・講評は,本誌2021年4月号にてご確認ください.