出題(2021年3月号掲載分)/応募締切(3月8日)/解答(2021年6月号掲載)
出題1
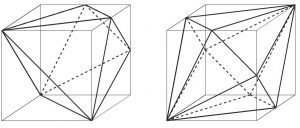 左は,1 辺の長さが 1 の立方体の,お互いに隣り合わない 3 頂点と,それらを含まない 3 辺の中点を頂点とする八面体です.右は,1 辺の長さが 1 の立方体の,相対する 2 頂点と,それらを含まない 6 辺の中点を頂点とする十二面体です.
左は,1 辺の長さが 1 の立方体の,お互いに隣り合わない 3 頂点と,それらを含まない 3 辺の中点を頂点とする八面体です.右は,1 辺の長さが 1 の立方体の,相対する 2 頂点と,それらを含まない 6 辺の中点を頂点とする十二面体です.
(1) 左の八面体が,互いに直交する 3 直線の交点の両側で,交点から 1 と $\dfrac 12$ の点を頂点とする八面体と合同であることを示してください.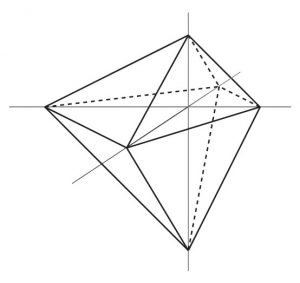
(2) 1 辺の長さが 2 の立方体に,左の八面体 6 個と右の十二面体 3 個を入れる方法を考えてください.全部で 8 個なら自明ですが, 9 個あります.どうやったら入るのでしょうか.
出題:立木秀樹
出題2
有名な無限級数に関する式の,カラビによる超短証明として知られた次の等式
\begin{align*}
\sum^\infty_{n=1}\frac 1{(2n-1)^2}
=\int^1_0\int^1_0\frac 1{1-x^2y^2}\,dxdy
=\frac{\pi^2}8
\end{align*}は,上記の二重積分を次のように巧みな変数変換
\begin{align*}
x=\frac{\sin\alpha}{\cos\beta},\quad
y=\frac{\sin\beta}{\cos\alpha}
\end{align*}することにより,二辺が $\dfrac\pi2$ の直角二等辺三角形の面積を計算して示せます.そこで,この超短証明を参考にして,その三次元版を考察していただきます.
(1)
\begin{align*}
\sum^\infty_{n=1}\frac{(-1)^{n-1}}{(2n-1)^3}
=\int^1_0\int^1_0\int^1_0
\frac 1{1+x^2y^2z^2}\,dxdydz
=\frac{\pi^3}{32}
\end{align*}が成り立つことを,ある空間の領域 (多面体) $D_1$ の体積を計算することによって示してください.
(2)無限級数
\begin{align*}
\varphi(3)=\sum^\infty_{n=1}\frac 1{(2n-1)^3}
=\int^1_0\int^1_0\int^1_0
\frac 1{1-x^2y^2z^2}\,dxdydz
\end{align*}の値がある空間の領域 $D_2$ の体積に一致するように,$D_2$ の定義式を求めてください.ちなみに,$\varphi(3)$ の正確な値は未だ決定されていません.
出題:佐久間一浩
応募規定[解答掲載2021年6月号]
郵送の場合
B5判の用紙をご使用のうえ,解答用紙 l 枚ごとにA:出題の番号(例:3月号出題1),B:住所,氏名(ふりがなも明記,誌上での仮名を希望される方は,こちらに明記),年齢,職業を記入して,下記宛先までお送りください.
〒170-8474 東京都豊島区南大塚3-12-4
日本評論社 数学セミナー〈エレガントな解答をもとむ〉係
メール送信の場合
B5判のサイズで,解答用紙l枚ごとにA:出題の番号(例:3月号出題1),B:住所,氏名(ふりがなも明記,誌上での仮名を希望される方は,こちらに明記),年齢,職業を記入して,下記フォームから PDF ファイルを送信して下さい (ファイルサイズ10MBまで).
解答記載に LaTeX ご利用の方は,テンプレートもご活用下さい.テンプレート利用は任意です.またテンプレートの漢字コードはUTF8です.ファイルが文字化けするときは適宜変換してお使いください.
投稿フォームが上手く動かないなどの場合は,susemi_elegant@nippyo.co.jp に直接お送り下さい.
注意事項
- 締切:2021年3月8日
- 二題に応募されるときは,郵送の場合は解答用紙を,メール送信の場合はファイルを,出題ごとにかえてください.
- 年齢を忘れずにお書きください.
- 解答用紙は両面の使用を不可とします.
- 解答用紙はご返却できません.
- 問題のご感想も歓迎します.
- 出題掲載号:数学セミナー2021年3月号
- 解答・講評は,本誌2021年6月号にてご確認ください.





