Web日本評論 > 日評雑誌記事セレクション > 出題（2022年12月号掲載分）／応募締切（12月8日）／解答（2023年3月号掲載）

出題（2022年12月号掲載分）／応募締切（12月8日）／解答（2023年3月号掲載）

エレガントな解答をもとむ(数学セミナー)｜ 2022.11.09

『数学セミナー』のコーナー「エレガントな解答をもとむ」の出題を掲載します．奮ってご応募ください．解答・講評(3ヶ月後)は，本誌にてご確認ください．

(毎月10日頃の掲載予定)

$\def\t#1{\text{#1}}\def\dfrac#1#2{\displaystyle\frac{#1}{#2}}$

出題1

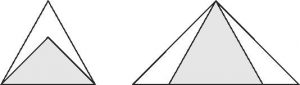
正 3 角形の中に直角 2 等辺 3 角形を収めるとき，下図左のようにすると面積が占める割合は最大になり，その値は $\dfrac1{\sqrt{3}}$ です．反対に，直角 2 等辺 3 角形の中に正 3 角形を収めるとき，下図右のようにすると最大になり，その値も同じく $\dfrac1{\sqrt{3}}$ です．

これは偶然の一致でしょうか．そこで，次の問題を取り上げてみます．

互いに相似でない任意の 3 角形 $\t{ABC}$ と 3 角形 $\t{DEF}$ を考えます．そして，3 角形 $\t{ABC}$ の相似形のうち，3 角形 $\t{DEF}$ に収まる最大の 3 角形を $\t A’\t B’\t C’$ とし，3 角形 $\t{DEF}$ の相似形のうち，3 角形 $\t{ABC}$ に収まる最大の 3 角形を $\t D’\t E’\t F’$ とするとします．このとき，次の等式はつねに成り立つでしょうか．
\begin{align*}
\frac{\text{3 角形 $\t A’\t B’\t C’$の面積}}{\text{3 角形 $\t{DEF}$ の面積}}
=
\frac{\text{3 角形 $\t D’\t E’\t F’$ の面積}}{\text{3 角形 $\t{ABC}$ の面積}}
\end{align*}

もしつねに成り立つとしたら，そのことを証明してください．成り立たないとしたら，反例を見つけ，それが反例であることを証明してください．

等式が成立する必要条件や十分条件がわかったなど，本問の一部のみが解けた場合の答案提出も歓迎です．

出題：岩沢宏和

$\def\Z{\mathbf{0}}\def\I{\mathbf{1}}\def\co{c}$

出題2

集合 $\varOmega=\{\varepsilon,0,1,00,\cdots\}$ を，$0$ と $1$ からなる有限文字列の全体とします．$\varepsilon$ は長さ $0$ の文字列です．

有限文字列 $w$ と $w’$ を連結した文字列を $ww’$ と書きます．また部分集合 $A,\,B\subseteqq \varOmega$ について，連結 $A\cdot B$ を $A\cdot B=\{ww’\mid w\in A,\, w’\in B\}$ とします．

正規表現は，以下のように再帰的に定義されます．

$\Z$ と $\I$ は正規表現である．
$r$ と $s$ が正規表現のとき，和 $r+s$，積 $r\cdot s$，スター $r^{\ast}$ と補 $r^{\co}$ も正規表現である．

正規表現 $r$ には，($r$ にマッチする言語と呼ばれる) $\varOmega$ の部分集合 $L(r)$ が以下で再帰的に定義されます．

$L(\Z)=\{0\}$ と，$L(\I)=\{1\}$．
$L(r+s)=L(r)\cup L(s),\,L(r\cdot s)=L(r)\cdot L(s),\,L(r^{\ast})=\{\varepsilon\}\cup L(r)\cup (L(r)\cdot L(r))\cup\cdots$ と，$L(r^{\co})=\varOmega\setminus L(r)$ (ここで $r$ と $s$ は正規表現)．

特に $L(r^{\ast})$ は $L(r)$ の任意有限回の繰り返し，$L(r^{\co})$ は $L(r)$ の補集合です．例えば $\varOmega=L（(\Z+\I)^{\ast}）$ です．

問題 1　正規表現 $(\I^{\co}\cdot \I)^{\ast}$ を，スターが登場しない正規表現で書き直してください．

問題 2　正規表現 $（(\Z+\I)\cdot \Z^{\ast}\cdot \I）^{\ast}$ を，スターの入れ子が登場しない正規表現で書き直してください．

例えば $L(\Z^{\ast}+\Z^{\co})=L(\Z+\Z^{\co})\ (=\varOmega)$ なので，$\Z^{\ast}+\Z^{\co}$ はスターを 1 回も使わない $\Z+\Z^{\co}$ で書き直せています．また問題 2 のような書き直しの例としては，$L（(\Z+(\I\cdot(\Z+\I))^{\ast})^{\ast}）=L(((\I^{\co}\cdot \I)^{\co})^{\ast})$ があります．

出題：土岡俊介