出題(2024年5月号掲載分)/応募締切(5月8日)/解答(2024年8月号掲載)
出題1
P(x) を有理数係数の 3 次多項式とする.このとき,P(Q(x)) が可約となるような有理数係数の 2 次多項式 Q(x) が存在することを証明せよ.
ただし,有理数係数の多項式 R(x) が可約であるとは,定数でない有理数係数の多項式 R1(x),R2(x) であって R(x)=R1(x)R2(x) を満たすものが存在することをいう.
出題:斎藤新悟 (九州大学基幹教育院)
出題2
n を 2 以上の自然数として,R={0,1,⋯,n−1} とします.n 次正方行列 A の各行および各列に n 個の R の異なる数が一つずつ入るとき,A を方陣と見立てて R 上のラテン方陣または n 次ラテン方陣とよびます.
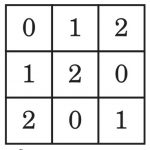
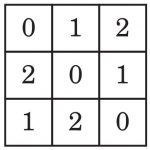
R 上のラテン方陣 A と B について,同じ位置のセルに入る数の対全体が,R の任意の 2 要素 x と y の対 (x,y) のすべて (n2 個ある) にわたるとき,A と B は互いに直交するといいます.例えば 3 次のラテン方陣
は,同じ位置のセルに入る数の対全体が (0,0),(0,1),(0,2),(1,0),(1,1),(1,2),(2,0),(2,1),(2,2) のすべてにわたるので,互いに直交しています.
(1) 1 より大きい奇数 n に対し,互いに直交する 2 つの n 次ラテン方陣を構成しその構成手順を記してください.
(2) 3 より大きい素数 p に対し,3 つの 4p 次ラテン方陣でそのうちのどの 2 つも互いに直交するようなものを構成してください.
余力のある方は互いに直交する 2 つの 10 次ラテン方陣の構成にチャレンジしてみてください.
出題:中川暢夫 (近畿大学理工学部)
応募規定[解答掲載2024年8月号]
郵送の場合
B5判の用紙をご使用のうえ,解答用紙 1 枚ごとにA:出題の番号(例:5月号出題1),B:住所,氏名(ふりがなも明記,誌上での仮名を希望される方は,こちらに明記),年齢,職業を記入して,下記宛先までお送りください.
〒170-8474 東京都豊島区南大塚3-12-4
日本評論社 数学セミナー〈エレガントな解答をもとむ〉係
メール送信の場合
B5判のサイズで,解答用紙 1 枚ごとにA:出題の番号(例:5月号出題1),B:住所,氏名(ふりがなも明記,誌上での仮名を希望される方は,こちらに明記),年齢,職業を記入して,下記フォームから PDF ファイルを送信して下さい (ファイルサイズ10MBまで).
解答記載に LaTeX ご利用の方は,テンプレートもご活用下さい.テンプレート利用は任意です.またテンプレートの漢字コードはUTF8です.ファイルが文字化けするときは適宜変換してお使いください.
(1)投稿フォームが上手く動かない,(2)受信確認メール希望の方でメールが届かない,などの場合,susemi_elegant@nippyo.co.jp に直接お送り下さい.
注意事項
- 締切:2024年5月8日
- 二題に応募されるときは,郵送の場合は解答用紙を,メール送信の場合はファイルを,出題ごとにかえてください.
- 年齢を忘れずにお書きください.
- 解答用紙は両面の使用を不可とします.
- 解答用紙はご返却できません.
- 問題のご感想も歓迎します.
- 出題掲載号:数学セミナー2024年5月号
- 解答・講評は,本誌2024年8月号にてご確認ください.
「エレガントな解答をもとむ」をすべて見る
最新の「エレガントな解答をもとむ」はこちら