出題(2024年6月号掲載分)/応募締切(6月8日)/解答(2024年9月号掲載)
【「エレガントな解答をもとむ」(6月号出題)のWeb応募の不具合について(6/7 14時時点)】
6/4(火)から,弊社のメールサーバーのトラブルが生じており,ドメイン @nippyo.co.jp のメールアドレスで,メールが受信できない状況が続いています.
それに伴い,本ページで応募いただいている「エレガントな解答をもとむ」の解答が,6/5(水)の早朝以降,編集部で確認できない状況です.
6/5(水)の早朝から6/7(金)14時現在までの間,Web日本評論からご応募いただいた方は,お手数をおかけしますが,下記の電話番号までご一報ください.
[受付時間]
平日9:30~17:00[電話番号(数学セミナー編集部)]
03-3987-8599このたびはご不便をおかけしており,まことに申し訳ございません.
これからWebでご応募される方については,いったん解答の送付をお待ちいただくようお願いいたします.
Web応募については,締切を数日延期することを予定しております.進展等がありましたら,弊社ホームページ,Web日本評論,Xの小誌公式アカウントにて告知いたします.
【追記(6/7 17:00)】
6/7(金)15:40より,Web日本評論からご応募いただいた解答は編集部で確認できるように復旧いたしました.
なお,今回の6月号出題のWeb応募に限り,6/10(月)23:59まで締切を延期いたします.
また,6/5(水)9時ごろ~6/7(金)15時半ごろの間の応募で,今回のトラブルでご解答内容が確認できなかった方のうち,解答フォームにメールアドレスをご記載いただいた方へ確認のメールをお送りしています.
該当する方でメールが届いていない方,フォームにメールアドレスを記載されなかった方は,お手数ですが上記の電話番号にご連絡ください.
出題1
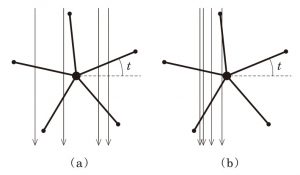
図のように,長さ 1 の羽根が等間隔に p 枚並んだ風車を原点に置き,その回転位置を t[rad] とする.y 軸方向真上から偶数 2k 本の矢が,x 座標 −1≦x≦1 の範囲に一様ランダムに落ちてくるとき,2k 本すべての矢に貫通される羽根の枚数の期待値 E2kp(t) を考える.たとえば,図 (a) の場合はすべての矢に貫通される羽根は 0 枚で,図 (b) の場合は 2 枚である.E2kp(t) の値は t の関数であるが,p,2kがある条件を満たせば,E2kp(t) は t によらない定数となる.その条件と,そのときの定数とを求めよ.
また,x 軸方向右側からも −1≦y≦1 の範囲に一様ランダムに 2k 本の矢がやってくるとき,2k 本すべての矢に貫通される羽根の枚数の期待値を F2kp(t) とする.これは単に F2kp(t)=E2kp(t+π2) である.E2kp(t)+F2kp(t) が定数関数になるときについても,前問と同様に考察せよ.
出題:山田修司 (京都産業大学理学部)
出題2
n を 3 以上の自然数とする.
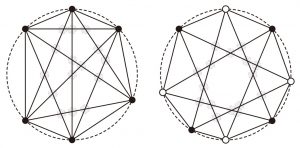
(1) n 個の頂点を円周上に配置し,どの頂点もほかのすべての頂点と直線分で結びます.このとき,辺の交差点の数を求めてください.
(2) n 個の白頂点と n 個の黒頂点を円周上に交互に配置し,どの白頂点もすべての黒頂点に直線分で結びます.このとき,辺の交差点の数を求めてください.
(1) 2 つの直線分の端点での接触は交差点と見なさない.
(2) 頂点は, 3 本以上の直線分が同一の交差点を持たないように,円周上に配置されている.
上の図では,左に (1) の n=6 の場合,右に (2) の n=4 の場合をそれぞれ示しており,各交差点をグレーの円でマークしています.
エレガントな解答を期待しています.
出題:中本敦浩 (横浜国立大学大学院環境情報研究院)
応募規定[解答掲載2024年9月号]
郵送の場合
B5判の用紙をご使用のうえ,解答用紙 1 枚ごとにA:出題の番号(例:6月号出題1),B:住所,氏名(ふりがなも明記,誌上での仮名を希望される方は,こちらに明記),年齢,職業を記入して,下記宛先までお送りください.
〒170-8474 東京都豊島区南大塚3-12-4
日本評論社 数学セミナー〈エレガントな解答をもとむ〉係
メール送信の場合
B5判のサイズで,解答用紙 1 枚ごとにA:出題の番号(例:6月号出題1),B:住所,氏名(ふりがなも明記,誌上での仮名を希望される方は,こちらに明記),年齢,職業を記入して,下記フォームから PDF ファイルを送信して下さい (ファイルサイズ10MBまで).
解答記載に LaTeX ご利用の方は,テンプレートもご活用下さい.テンプレート利用は任意です.またテンプレートの漢字コードはUTF8です.ファイルが文字化けするときは適宜変換してお使いください.
(1)投稿フォームが上手く動かない,(2)受信確認メール希望の方でメールが届かない,などの場合,susemi_elegant@nippyo.co.jp に直接お送り下さい.
注意事項
- 締切:2024年6月8日
- 二題に応募されるときは,郵送の場合は解答用紙を,メール送信の場合はファイルを,出題ごとにかえてください.
- 年齢を忘れずにお書きください.
- 解答用紙は両面の使用を不可とします.
- 解答用紙はご返却できません.
- 問題のご感想も歓迎します.
- 出題掲載号:数学セミナー2024年6月号
- 解答・講評は,本誌2024年9月号にてご確認ください.
「エレガントな解答をもとむ」をすべて見る
最新の「エレガントな解答をもとむ」はこちら