出題(2024年7月号掲載分)/応募締切(7月8日)/解答(2024年10月号掲載)
出題1
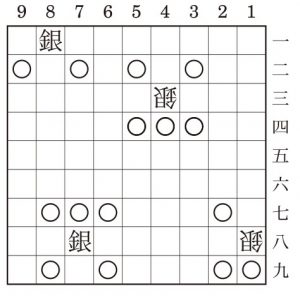
将棋の「銀」の駒を使った問題です.銀は前方,斜め前方,斜め後方のいずれかに動ける駒です (図 1 の○印に動けます) .なおここでは将棋と違い,銀が「成る」ことはできないものとします.
問1 この銀を最初に先手は 9 九,後手は 1 一に置き (図 2),先手と後手が交互に銀を動かして相手の銀を取ったら勝ちというルールのゲームを行うとすると,このゲームは後手必勝,すなわち後手が最善を尽くせば有限手数で先手の銀を必ず取れることを確認してください.
問2 最初に先手と後手の銀を置く地点それぞれについて,このゲームの結論が先手必勝,引き分け,後手必勝のいずれになるかを述べてください.
本問のアイデアは本誌にも何度も登場されている若島正さん (詰将棋作家,英文学者) ご提案の将棋パズルからです.解答は問 2 だけで結構です.なお将棋では駒の位置を算用数字と漢数字で表しますが,解答内では適宜座標設定をしていただいてかまいません.また,本問では $9 \times9$ サイズの盤で行う設定にしていますが,結論の証明はできるだけ一般の長方形の盤でも成り立つものを考えてみてください.
出題:篠田正人 (奈良女子大学研究院自然科学系)
出題2
(1) $X=\{1,2,\cdots,15\}$ とおく.A 君は $X$ の部分集合 $A_1,A_2,\cdots,A_{1000}$ で,任意の相異なる $i,\,j$ について
\begin{align}
|A_i\triangle A_j|\geqq 3 \tag{$\ast$}
\end{align}をみたすものを見つけた.これを聞いた B 君は A 君の情報から,$X$ の部分集合 $B_1,B_2,\cdots,B_{500}$ で,任意の相異なる $i,\,j$ について
\begin{align}
\text{$|B_i\triangle B_j|\geqq 3$ かつ $B_i\not\subset B_j$ かつ $B_i\not\supset B_j$} \tag{$\ast\ast$}
\end{align}をみたすものがあることに気づいた. B 君はどのように考えたのだろうか?
(2) 整数 $l\geqq 3$ について $n=2^l-1,\,X=\{1,2,\cdots,n\},\,s=2^{n-l}$ とおく.$X$ の部分集合 $A_1,A_2,\cdots,A_{s}$ で,任意の相異なる $i,\,j$ について ($\ast$) をみたすものが知られている.この事実を利用して,$X$ の部分集合 $B_1,B_2,\cdots,B_t$ で,任意の相異なる $i,\,j$ について ($\ast\ast$) をみたし,かつ $t>2^{n}/ (n\sqrt n)$ となるものがあることを示せ.
(1) のみの解答も歓迎します.なお,集合 $A,\,A’$ に対して $A\triangle A’=\{a:a\in A\cup A’\text{ かつ }a\not\in A\cap A’\}$ と定め,$|A|$ は集合 $A$ の要素の個数を表します.
出題:徳重典英 (琉球大学教育学部)
応募規定[解答掲載2024年10月号]
郵送の場合
B5判の用紙をご使用のうえ,解答用紙 1 枚ごとにA:出題の番号(例:7月号出題1),B:住所,氏名(ふりがなも明記,誌上での仮名を希望される方は,こちらに明記),年齢,職業を記入して,下記宛先までお送りください.
〒170-8474 東京都豊島区南大塚3-12-4
日本評論社 数学セミナー〈エレガントな解答をもとむ〉係
メール送信の場合
B5判のサイズで,解答用紙 1 枚ごとにA:出題の番号(例:7月号出題1),B:住所,氏名(ふりがなも明記,誌上での仮名を希望される方は,こちらに明記),年齢,職業を記入して,下記フォームから PDF ファイルを送信して下さい (ファイルサイズ10MBまで).
解答記載に LaTeX ご利用の方は,テンプレートもご活用下さい.テンプレート利用は任意です.またテンプレートの漢字コードはUTF8です.ファイルが文字化けするときは適宜変換してお使いください.
(1)投稿フォームが上手く動かない,(2)受信確認メール希望の方でメールが届かない,などの場合,susemi_elegant@nippyo.co.jp に直接お送り下さい.
注意事項
- 締切:2024年7月8日
- 二題に応募されるときは,郵送の場合は解答用紙を,メール送信の場合はファイルを,出題ごとにかえてください.
- 年齢を忘れずにお書きください.
- 解答用紙は両面の使用を不可とします.
- 解答用紙はご返却できません.
- 問題のご感想も歓迎します.
- 出題掲載号:数学セミナー2024年7月号
- 解答・講評は,本誌2024年10月号にてご確認ください.
「エレガントな解答をもとむ」をすべて見る
最新の「エレガントな解答をもとむ」はこちら