• #エレガント
• #数セミ
• #数学

 『数学セミナー』のコーナー「エレガントな解答をもとむ」の出題を掲載します．奮ってご応募ください．解答・講評(3ヶ月後)は，本誌にてご確認ください．

(毎月10日頃の掲載予定)

出題1

つぎの連立方程式を解いてください：
$$\begin{align*} \left\{\begin{array}{l} &\dfrac{2x}{1-x^2}=y,\\[5pt] &\dfrac{2y}{1-y^2}=z,\\[5pt] &\dfrac{2z}{1-z^2}=w,\\[5pt] &\dfrac{2w}{1-w^2}=x. \end{array} \right. \end{align*}$$

出題：渋川元樹 (神戸大学大学院理学研究科)

出題2

以下の図形 (グラフといいます) で，各 $\bigcirc$ に $1,\,2,\,3,\,4$ のいずれかの数字を割り当てて，次の 2 つの条件を満たすようにしたいと思います．

• 同じ数字が隣接しない．
• 各 $\bigcirc$ において，自分の数字と隣接する $\bigcirc$ のすべての数字の合計が奇数になる．

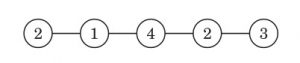
そのような数字の割り当てを，奇数和割り当てということにします．例えば，図 1 が奇数和割り当ての一例で，左から順に合計が $3,\, 7,\, 7,\, 9,\, 5$ となっています．

図1　奇数和割り当て

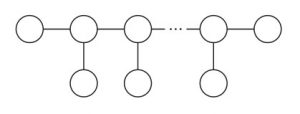
(1) $6$ 個の $\bigcirc$ が一直線上に並んでいる図 2 の図形に，奇数和割り当てを見つけてください．

(2)任意の正の整数 $n$ で，$n$ 個の $\bigcirc$ が図 2 のように一直線上に並んでいる図形に奇数和割り当てを見つけてください．

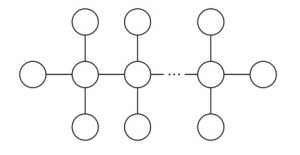
(3)図 3 や図 4 のような図形に，奇数和割り当てを見つけてください．

ほかのどのような図形 (特に，グラフ理論でいう木) に奇数和割り当てが存在するか，考えてもらえると嬉しいです．

図2　$6$ 個の丸

図3

図4

出題：小関健太 (横浜国立大学大学院環境情報研究院)

応募規定［解答掲載2025年7月号］

郵送の場合

B5判の用紙をご使用のうえ，解答用紙 1 枚ごとにA：出題の番号(例：4月号出題1)，B：住所，氏名(ふりがなも明記，誌上での仮名を希望される方は，こちらに明記)，年齢，職業を記入して，下記宛先までお送りください．

〒170-8474　東京都豊島区南大塚3-12-4
日本評論社　数学セミナー〈エレガントな解答をもとむ〉係

メール送信の場合

B5判のサイズで，解答用紙 1 枚ごとにA：出題の番号(例：4月号出題1)，B：住所，氏名(ふりがなも明記，誌上での仮名を希望される方は，こちらに明記)，年齢，職業を記入して，下記フォームから PDF ファイルを送信して下さい (ファイルサイズ10MBまで)．

解答記載に LaTeX ご利用の方は，テンプレートもご活用下さい．テンプレート利用は任意です．またテンプレートの漢字コードはUTF8です．ファイルが文字化けするときは適宜変換してお使いください．

(1)投稿フォームが上手く動かない，(2)受信確認メール希望の方でメールが届かない，などの場合，susemi_elegant@nippyo.co.jp に直接お送り下さい．

注意事項

• 締切：2025年4月8日
• 二題に応募されるときは，郵送の場合は解答用紙を，メール送信の場合はファイルを，出題ごとにかえてください．
• 年齢を忘れずにお書きください．
• 解答用紙は両面の使用を不可とします．
• 解答用紙はご返却できません．
• 問題のご感想も歓迎します．
• 出題掲載号：数学セミナー2025年4月号
• 解答・講評は，本誌2025年7月号にてご確認ください．

「エレガントな解答をもとむ」をすべて見る
最新の「エレガントな解答をもとむ」はこちら

単行本が発売になりました！

• エレガントな解答をもとむ 名作セレクション 2000〜2020

• #エレガント
• #数セミ
• #数学